[Java] 백준(실버-4) 24060번 - 병합정렬 1

문제 풀이
문제 풀기에 앞서 병합정렬에 대해서 알아보자.
병합정렬이란?
기본적으로 분할 정복 알고리즘을 기반하여 정렬하는 방식으로 문제를 분할하고, 분할한 문제를 정복하여 병합하는 과정이다.
원소가 저장되어 있는 배열을 계속 쪼개서 길이가 1인 배열을 만들고, 이후 정렬하면서 합치는 알고리즘이다.
병합정렬 과정
- 주어진 배열을 절반으로 분할한다. 즉 부분배열로 나눈다.
- 부분배열의 길이가 1이 될 때까지 1번 과정을 반복한다.
- 인접한 부분배열의 원소를 비교하며 정렬하여 합친다.
아래 그림을 참고하면 이해하기 쉽다.
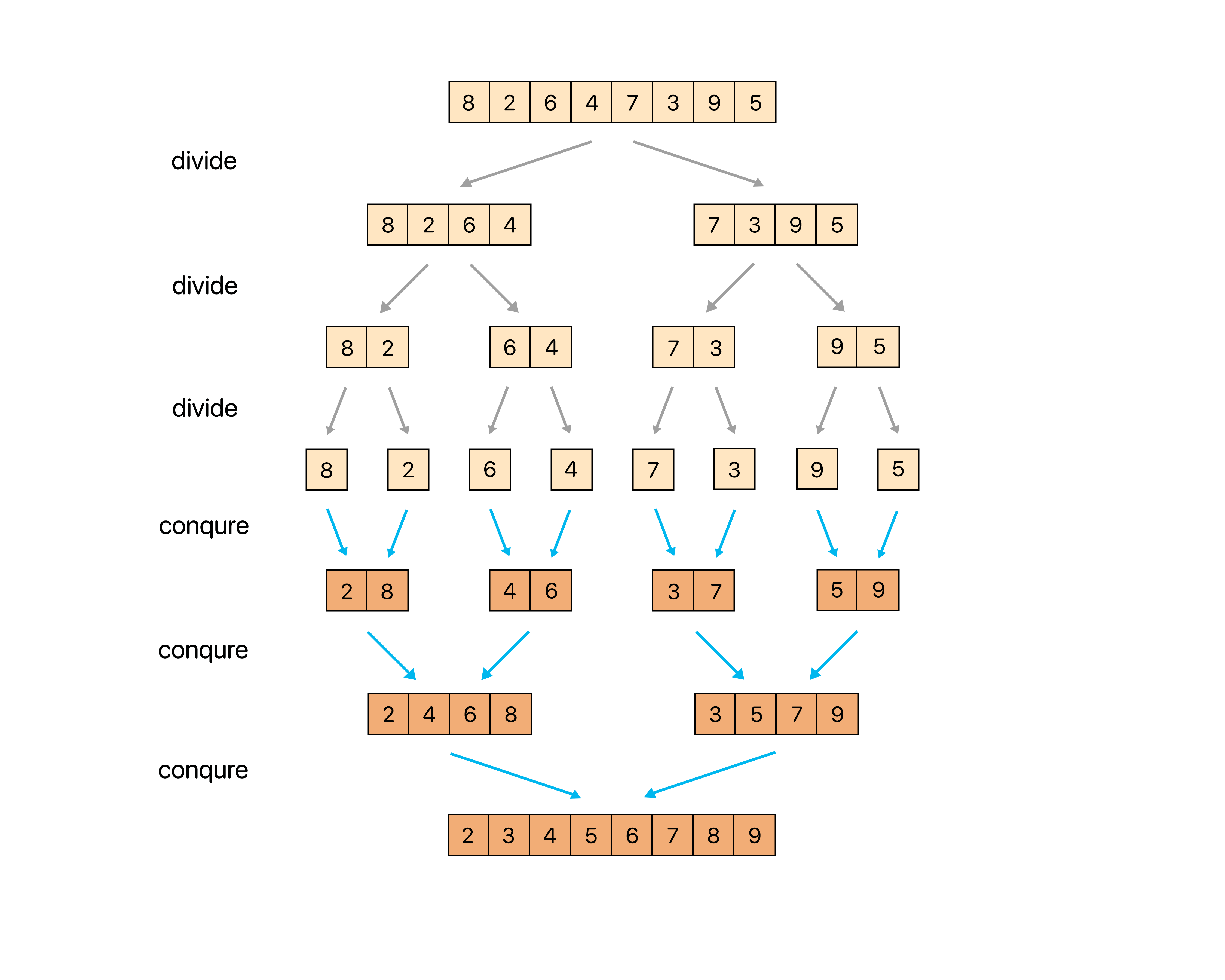
그리고 장단점도 함께 살펴보자.
병합정렬의 장점 및 단점
[장점]
- 최선과 최악의 경우 모두 O(NlogN)의 시간복잡도를 가진다.
- 안정된 정렬 방법이다.
[단점]
- 별도로 배열을 이용하기에 메모리 사용량이 높다.
- 데이터가 많을 경우 원본배열로 정렬된 데이터를 덮어씌우는 과정에서 시간이 많이 소요된다.
이와 같이 병합정렬에 대해서 알아보았으니 실제로 구현을 해보자.
이 문제의 요구사항은 병합정렬 중 K번째로 병합되어 저장된 수를 구하는 것이다.
아이디어 도출
문제 요구사항을 만족하기 위해 생각한 아이디어는 다음과 같다.
- 주어진 배열을 가지고 병합정렬 작업을 진행한다.
- 병합정렬 중 K번째로 저장된 수를 구한다.
- K번째로 저장된 수가 없다면 -1를 반환한다.
이제 코드를 작성해보자.
1
2
3
4
public static int[] sorted_arr;
public static int cnt = 0;
public static int K = 0;
public static int res = 0;
먼저 Main 클래스 내에서 사용할 static 변수들을 선언하자.
분해하여 정렬된 데이터들을 저장할 임시 배열 sorted_arr를 선언하고 저장횟수를 기록할 cnt 변수, 입력받을 K를 저장할 K변수, K번째 저장된 수 res 변수를 초기화한다.
1
2
3
4
5
6
7
8
9
int N = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
String[] str_arr = br.readLine().split(" ");
int[] arr = Arrays.stream(str_arr).mapToInt(Integer::parseInt).toArray(); // int형 배열로 변환
sort(arr);
if(cnt < K) res = -1;
bw.write(res+"\n");
그리고 main 메서드에서 N과 K, 주어진 수들을 입력받아 int형 arr 배열까지 만든 뒤, sort() 함수를 실행하여 병합정렬을 실행한다.
병합정렬 실행 후 cnt(저장횟수)가 K보다 작다면 -1를 반환하면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static void sort(int[] arr) {
// l은 첫번째 인덱스, r은 마지막 인덱스, m은 중간 인덱스
sorted_arr = new int[arr.length]; // 정렬 배열 초기화
merge_sort(arr, 0, arr.length-1);
}
public static void merge_sort(int[] arr, int l, int r) {
if(l == r) return; // 부분 배열 원소가 1개일 경우 분해할 수 없기 때문에 반환
int m = (l + r) / 2; // 배열 중간 위치
merge_sort(arr, l, m); // 첫번째부터 절반까지의 왼쪽 배열 (l ~ m)
merge_sort(arr, m+1, r); // 절반 이후부터 마지막까지 오른쪽 배열 (m+1 ~ r)
merge(arr, l, m, r); // 병합 작업 진행
}
sort() 함수에서는 정렬하여 분해한 배열을 저장할 sorted_arr 배열을 초기화한다. sorted_arr 배열의 경우 앞서 static으로 선언하였기에 전역으로 관리할 수 있다.
그리고 merge_sort() 함수에 정렬할 배열 arr과 투 포인터로 이용할 값을 넘겨준다.
merge_sort() 함수에서는 매개변수로 받은 투 포인터 값을 통해 첫번째 원소부터 절반까지의 원소를 통해 왼쪽 배열을 만들고, 절반 이후 원소부터 마지막 원소를 통해 오른쪽 배열을 만든다.
그렇게 분해하여 만든 부분배열들을 merge() 함수를 통해 병합 작업을 진행한다.
병합 작업을 진행할 merge() 함수 코드는 아래와 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public static void merge(int[] arr, int l, int m, int r) {
int left = l; // 왼쪽 배열 시작점
int right = m + 1; // 오른쪽 배열 시작점
int idx = l; // 정렬된 데이터가 저장될 인덱스
while(left <= m && right <= r) {
// 1. 왼쪽 배열 left번째 원소가 오른쪽 배열 right번째 원소보다 작거나 같다면
// 2. sorted_arr에 left번째 원소를 저장하고 left, idx를 1 증가시킨다.
if(arr[left] <= arr[right]) {
sorted_arr[idx] = arr[left];
idx++;
left++;
}
// 3. 오른쪽 배열 right번째 원소가 왼쪽 배열 left번째 원소보다 작거나 같다면
// 4. sorted_arr에 right번째 원소를 저장하고 right, idx를 1 증가시킨다.
else {
sorted_arr[idx] = arr[right];
idx++;
right++;
}
}
// 5. 왼쪽 배열의 원소가 모두 sorted_arr에 채워졌다면 나머지 자리에 오른쪽 배열을 차례대로 저장한다.
if(left > m) {
while(right <= r) {
sorted_arr[idx] = arr[right];
idx++;
right++;
}
}
// 6. 오른쪽 배열의 원소가 모두 sorted_arr에 채워졌다면 나머지 자리에 왼쪽 배열을 차례대로 저장한다.
else {
while(left <= m) {
sorted_arr[idx] = arr[left];
idx++;
left++;
}
}
// 7. 병합하여 정렬된 sorted_arr배열을 기존 arr배열에 덮어씌운다.
for(int i=l; i<=r; i++) {
cnt++; // 저장횟수
if(cnt == K) res = sorted_arr[i]; // K번째 저장된 수
arr[i] = sorted_arr[i];
}
}
[1,2,3,4번 과정]
병합 작업에서는 왼쪽 배열의 첫번째 원소부터 절반까지 원소를 오른쪽 배열의 원소와 비교해가며 작거나 같다면 sorted_arr 새 배열에 첫번째 자리부터 저장해나간다.
또한 마찬가지로 오른쪽 배열의 첫번째 원소부터 마지막까지의 원소를 왼쪽 배열의 원소와 비교해가며 작거나 같다면 sorted_arr 새 배열에 첫번째 자리부터 저장해나간다.
그런데 왼쪽 배열이나 오른쪽 배열에 원소가 모두 반대쪽 배열의 원소보다 작아 먼저 새 배열에 저장되는 경우가 있다.
[1,2,4,5,9,11,25,75]와 같은 배열이 부분배열이 만들어졌다면 앞 왼쪽 배열 원소 모두가 먼저 새 배열에 저장되어 오른쪽 배열 원소가 남게 된다.
[5,6번 과정]
위와 같은 경우를 대비해 왼쪽 배열이나 오른쪽 배열의 원소가 먼저 sorted_arr에 저장되었다면 결국 나머지 배열의 원소를 차례대로 저장하면 된다.
[7번 과정]
그렇게 정렬된 새 sorted_arr 배열을 기존 배열인 arr 배열에 덮어씌워야 한다.
여기서 전역변수인 cnt에 저장횟수를 증가시키면서 저장시키고, cnt가 K와 같다면 res 변수에 K번째 저장된 수를 담으면 된다.
이후 main 메서드에서 cnt와 K를 비교하여 res 값을 정한 뒤 출력하면 K번째 저장된 수를 출력할 수 있다.
1
2
if(cnt < K) res = -1;
bw.write(res+"\n");
작성코드
추후 복습을 위해 이번 문제 작성코드는 주석을 많이 달아놓았다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
import java.io.*;
import java.util.*;
class Main {
public static int[] sorted_arr;
public static int cnt = 0;
public static int K = 0;
public static int res = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
String[] str_arr = br.readLine().split(" ");
int[] arr = Arrays.stream(str_arr).mapToInt(Integer::parseInt).toArray(); // int형 배열로 변환
sort(arr);
if(cnt < K) res = -1;
bw.write(res+"\n");
bw.flush();
bw.close();
br.close();
}
public static void sort(int[] arr) {
// l은 첫번째 인덱스, r은 마지막 인덱스, m은 중간 인덱스
sorted_arr = new int[arr.length]; // 정렬 배열 초기화
merge_sort(arr, 0, arr.length-1);
}
public static void merge_sort(int[] arr, int l, int r) {
if(l == r) return; // 부분 배열 원소가 1개일 경우 분해할 수 없기 때문에 반환
int m = (l + r) / 2; // 배열 중간 위치
merge_sort(arr, l, m); // 첫번째부터 절반까지의 왼쪽 배열 (l ~ m)
merge_sort(arr, m+1, r); // 절반 이후부터 마지막까지 오른쪽 배열 (m+1 ~ r)
merge(arr, l, m, r); // 병합 작업 진행
}
public static void merge(int[] arr, int l, int m, int r) {
int left = l; // 왼쪽 배열 시작점
int right = m + 1; // 오른쪽 배열 시작점
int idx = l; // 정렬된 데이터가 저장될 인덱스
while(left <= m && right <= r) {
// 투 포인터 사용
// 1. 왼쪽 배열 left번째 원소가 오른쪽 배열 right번째 원소보다 작거나 같다면
// 2. sorted_arr에 left번째 원소를 저장하고 left, idx를 1 증가시킨다.
if(arr[left] <= arr[right]) {
sorted_arr[idx] = arr[left];
idx++;
left++;
}
// 1. 오른쪽 배열 right번째 원소가 왼쪽 배열 left번째 원소보다 작거나 같다면
// 2. sorted_arr에 right번째 원소를 저장하고 right, idx를 1 증가시킨다.
else {
sorted_arr[idx] = arr[right];
idx++;
right++;
}
}
// 왼쪽 배열의 원소가 모두 sorted_arr에 채워졌다면 나머지 자리에 오른쪽 배열을 차례대로 저장한다.
if(left > m) {
while(right <= r) {
sorted_arr[idx] = arr[right];
idx++;
right++;
}
}
// 오른쪽 배열의 원소가 모두 sorted_arr에 채워졌다면 나머지 자리에 왼쪽 배열을 차례대로 저장한다.
else {
while(left <= m) {
sorted_arr[idx] = arr[left];
idx++;
left++;
}
}
// 병합하여 정렬된 sorted_arr배열을 기존 arr배열에 덮어씌운다.
for(int i=l; i<=r; i++) {
cnt++;
if(cnt == K) res = sorted_arr[i];
arr[i] = sorted_arr[i];
}
}
}
회고
- O(NlogN)의 시간복잡도를 가지는 병합정렬에 대해 공부할 수 있었다. 분할 정복 알고리즘과 함께 자주 다뤄지는 정렬방식이라고 한다. 분할 정복 알고리즘에 대해서도 공부해야겠다.
