[Java] 백준(실버-1) 11729번 - 하노이의 탑 이동 순서
문제 풀이
하노이의 탑에서 원판을 이동시키는 원리는 워낙 유명했지만 잘 기억이 안나서 다시 찾아보았다.
하노이의 탑 원판 이동 조건
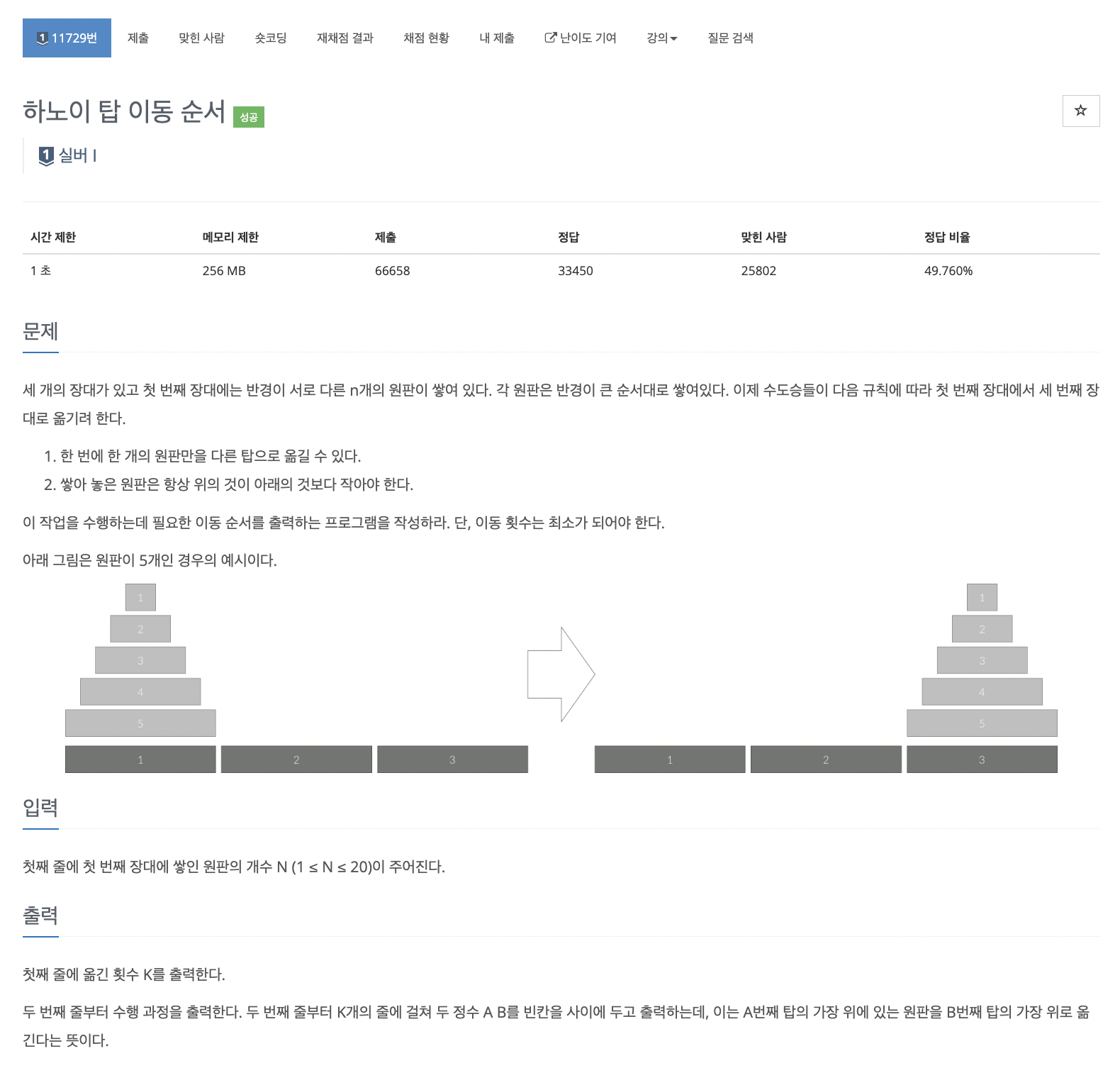
- 하노이의 탑은 위 그림과 같이 크기 가 다른 원반이 한 기둥에 놓여져 있고 원반을 모두 왼쪽에서 오른쪽으로 옮겨야 한다.
- 원반은 큰 것이 아래로 가게 쌓아야 하며 작은 원반 위에 큰 원반이 올 수 없다.
- 원반을 옮길 때에는 가장 위에 쌓여있는 원반 부터 옮겨야 한다.
문제 카테고리에서 주어진 대로 재귀 알고리즘을 이용해 3개의 탑에서 N개의 원판이 주어지면 첫번째 탑에서 마지막 탑까지 N개의 원판을 이동시켜야 한다.
하노이탑 이동조건에서의 핵심은 “작은 원판 위에 큰 원판은 올 수 없다.”라는 조건이다.
하노이탑 이동 원리
간단히 이동 원리를 살펴보자면,
- 첫번째 탑의 가장 큰 원판을 마지막 탑으로 옮기기 위해서는 N-1개의 원판이 첫번째 탑에서 중간 탑으로로 가야한다.
- 그러면 첫번째 탑에 있는 가장 큰 원판이 마지막 탑으로 이동할 수 있다.
- 가장 큰 원판이 마지막 탑으로 옮겨지면, 중간 탑에 있는 N-1개의 원판을 마지막 탑로 이동시키면 된다.
재귀함수 활용하기
재귀를 어떻게 활용해야할지 처음엔 감이 안잡혔지만, 곰곰히 생각해보니 단순하게 풀 수 있었다.
첫번째 탑에서 두번째 탑으로 이동해야할 N-1개의 원판들을 재귀함수를 호출하여 이동시키고, 남은 1개의 원판을 이동시킨 후 다시 재귀함수를 호출하면 된다.
말로 설명하자면 너무 어려운데, 간단히 의사코드를 작성하여 살펴보자.
1
2
3
4
5
6
7
8
9
10
11
12
하노이 함수(첫번째탑, 중간탑, 마지막탑, N) {
if(옮겨야할 원판이 1개라면) { // 2
이동 횟수 1증가
첫번째탑 마지막탑 출력
}
else {
하노이 함수(첫번째탑, 마지막탑, 중간탑, N-1) // 1
이동 횟수 1증가
첫번째탑 마지막탑 출력
하노이 함수(중간탑, 첫번째탑, 마지막탑, N-1) // 3
}
}
위왁 같이 계속 (1)첫번째 탑에서 중간 탑으로 이동하는 함수를 재귀호출하여 N-1개 원판을 이동하면 (2)이동해야 할 원판이 1개가 남고,
그 때 첫번째탑에서 마지막탑으로 이동했다는 것을 출력하고, (3)마지막으로 중간탑에 있는 N-1개의 원판을 마지막탑으로 이동하는 함수를 재귀호출하면 된다.
자 이제 위에서 작성한 의사코드를 통해 문제 솔루션 코드를 작성해보자.
1
2
static StringBuilder sb = new StringBuilder();
static int moveCnt = 0;
먼저 탑 이동 과정을 함수 수행후 출력해야 하기에 StringBuilder을 static으로 선언하여 사용할 것이다. 그리고 원판 이동 횟수를 담을 moveCnt 또한 static으로 선언하여 변수를 만들자.
1
2
3
4
int N = Integer.parseInt(br.readLine());
hanoi(1, 2, 3, N);
bw.write(moveCnt + "\n");
bw.write(sb.toString()+"\n");
원판 갯수 N을 입력받고 탑은 3개로 고정이니, hanoi 함수에 첫번째 탑 1, 중간 탑 2, 마지막 탑 3, N을 인자로 실행한다.
그리고 함수 수행 후 하노이탑 원판 이동횟수와 함수 내에서 StringBuilder에 담은 수행 과정을 출력하면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
public static void hanoi(int first, int center, int last, int N) {
if(N == 1) {
moveCnt++;
sb.append(first + " " + last + "\n");
}
else {
hanoi(first, last, center, N-1);
moveCnt++;
sb.append(first + " " + last + "\n");
hanoi(center, first, last, N-1);
}
}
마지막으로 hanoi 함수를 살펴보자. 의사코드에서 작성한 것과 동일하다.
예를 들어 hanoi(1,2,3,N=3)을 실행한다면, 2개의 원판을 중간 탑에 이동시킬 때까지 재귀호출을 하고, (이때 2개 원판을 이동시킬 때마다 이동횟수를 1씩 증가시키고 수행과정을 출력한다.)
2개의 원판을 모두 중간탑으로 이동시키고 원판이 1개 남는다면 마지막 탑으로 이동시키고 중간 탑에 있는 2개의 원판을 마지막 탑으로 옮기는 함수를 호출하면 된다.
여기서 중요한 점은 원판이 1개가 남을 때까지 재귀호출을 통해 이동시킨다는 점이다. 이 원리는 문제를 풀 때 정말 큰 도움이 되었다.
작성코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import java.io.*;
class Main {
static StringBuilder sb = new StringBuilder();
static int moveCnt = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
hanoi(1, 2, 3, N);
bw.write(moveCnt + "\n");
bw.write(sb.toString()+"\n");
bw.flush();
bw.close();
br.close();
}
public static void hanoi(int first, int center, int last, int N) {
if(N == 1) {
moveCnt++;
sb.append(first + " " + last + "\n");
}
else {
hanoi(first, last, center, N-1);
moveCnt++;
sb.append(first + " " + last + "\n");
hanoi(center, first, last, N-1);
}
}
}
회고
- 하노이의 탑의 원판이 이동하는 원리를 제대로 알고 있지 않아 원리 자체를 다시 공부하였다.
- 재귀 알고리즘을 통해 가장 작은 함수까지 재귀로 파고 들어가는 원리를 이해하면 쉽게 풀 수 있는 문제라고 생각이 들었다.
- 쌓인 순서대로 이동시켜야 한다는 점에서 stack을 활용해서도 풀 수 있는 문제라고 생각하여 추후 스택으로도 풀어봐야겠다.
