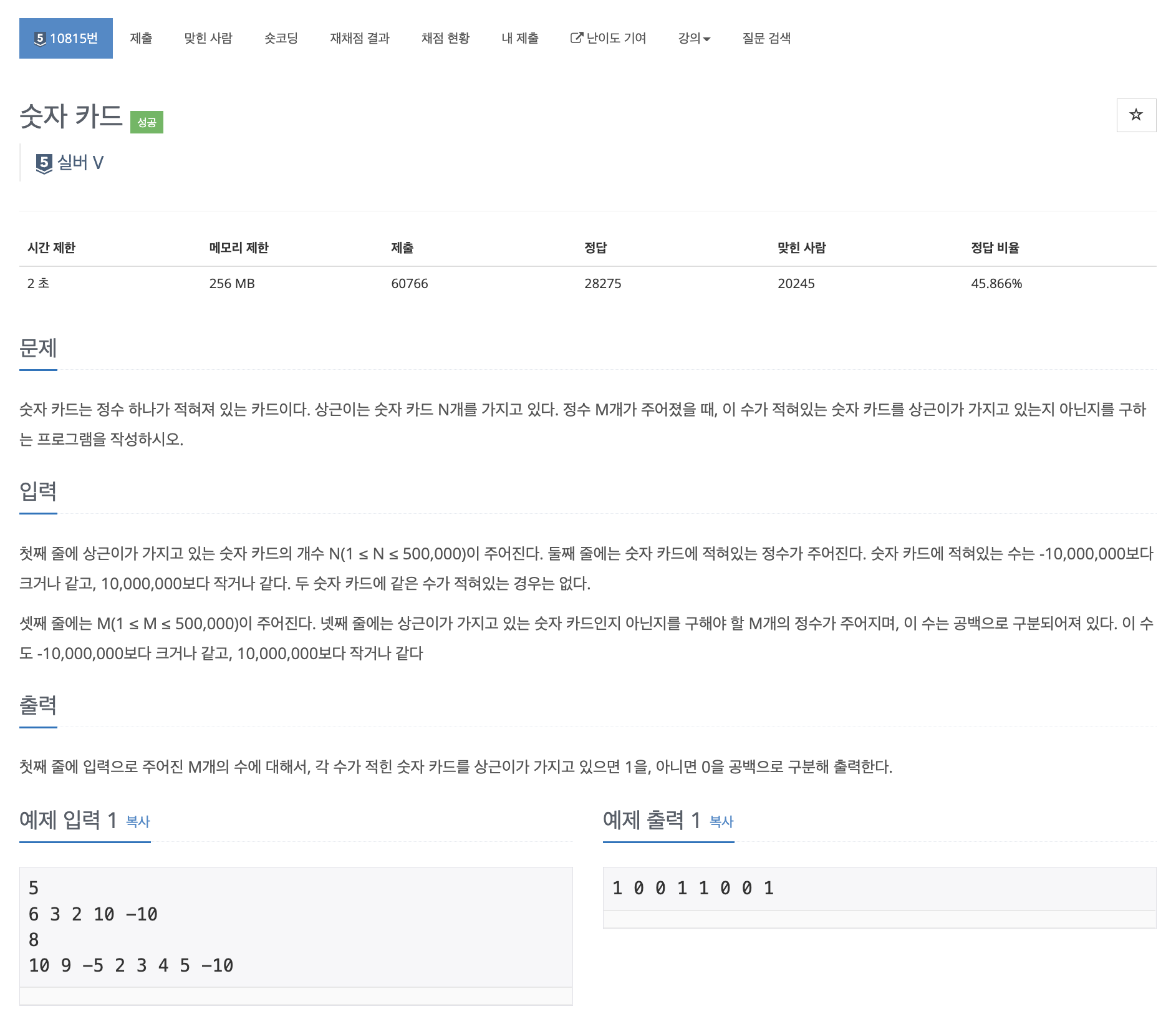
[Java] 백준(실버-5) 10815번 - 숫자 카드
문제 풀이
M개의 확인해야할 카드 중에서 N개의 카드들이 존재하는지 확인해야 한다.
나는 O(1)의 시간복잡도를 가지는 HashSet을 활용하여 N개의 카드중에 M개의 카드 각각이 존재하는지 여부를 따져서 정답을 낼 수 있었다.
이 문제는 선형탐색을 이용하면 시간복잡도가 O(n) 이기에 시간초과가 발생한다고 한다. 그렇기에 시간복잡도가 O(nlogn)인 이분탐색을 활용해야 한다고 한다.
그래서 이번 문제는 HashSet과 Arrays.binarySearch() 메서드(이분탐색)를 활용한 2가지 방식으로 풀어보았다.
HashSet 활용
HashSet을 사용한 이유는 add() 메서드와 contains() 메서드가 O(1)의 시간복잡도를 가지기에 빠른 실행시간을 보장할 것이라 판단하고 활용하였다.
바로 코드를 살펴보자.
1
2
3
4
5
6
7
HashSet<String> set = new HashSet<>();
int N = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
set.add(st.nextToken());
}
먼저 HashSet으로 사용할 set을 선언하고, N을 입력받아 set에 N개의 수들을 저장한다.
1
2
3
4
5
6
7
8
9
10
int M = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
for(int i=0; i<M; i++) {
String card = st.nextToken();
if(set.contains(card)) sb.append("1" + " ");
else sb.append("0" + " ");
}
그리고 M을 입력받고 M개의 수들을 탐색하며 set에 존재하는 수인지를 확인하여 StringBuilder에 1과 0을 담는다.
여기서 StringBuilder를 사용한 이유는 String보다 빠른 연산을 할 수 있기 때문이다.
이분탐색 활용
다음으로 문제에서 요구되는 대표적인 솔루션인 이분탐색을 이용하여 문제를 풀어보자.
이분탐색(=이진탐색, Binaey Search)이란?
정렬된 배열 또는 리스트에서 빠르게 탐색을 할 수 있는 방법이다.
- 배열의 중앙에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 배열에 있는지를 알아내어 탐색의 범위를 반으로 줄인다.
- 찾고자 하는 값이 속해있지 않은 부분은 전혀 고려할 필요가 없기 때문에, 매 단계에서 검색해야 할 리스트의 크기를 반으로 줄일 수 있다.
Java에서는 이분탐색 기능을 제공하는 라이브러리가 있다. 바로 Arrays 패키지 내의 binarySearch() 메서드이다.
Arrays.binarySearch()
Arrays 라이브러리 내 존재하는 binarySearch() 메소드는 정렬된 배열에서 매개변수로 넣은 값의 존재여부와 index 위치를 반환하며, 만약 존재하지 않는 값을 비교한다면 음수로 몇 번째 순서로 위치할지를 반환한다.
여기서 찾는 값이 존재한다면 양수이고 존재하지 않는다면 음수라면 점을 이용해 문제를 쉽게 풀 수 있다.
바로 코드를 작성해보자.
1
2
3
4
5
6
7
8
9
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
Arrays.sort(arr);
N을 입력받고 N만큼의 크기를 가진 arr 배열을 선언하자. 그리고 arr에 N개의 수들을 저장한다.
그리고 이분탐색의 전제조건으로 정렬된 배열을 넘겨주어야 하기 떄문에 arr배열을 정렬하자.
1
2
3
4
5
6
7
8
9
10
int M = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
for(int i=0; i<M; i++) {
int card = Integer.parseInt(st.nextToken());
if(Arrays.binarySearch(arr, card) >= 0) sb.append("1").append(" ");
else sb.append("0").append(" ");
}
그리고 M을 입력받고 M개의 수들을 순회하며 Arrays.binarySearch() 메서드를 활용해 M개의 수들이 앞서 저장한 arr 배열에 원소로 존재하는지를 확인한다.
만약 존재한다면 양수로 인덱스 위치를 반환할 것이고, 존재하지 않는다면 음수로 반환할 것이다. 그래서 반환값이 0보다 크거나 작다면 1을, 아니라면 0을 StringBuilder에 담으면 된다.
작성코드
작성코드 - HashSet 활용
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import java.io.*;
import java.util.*;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
HashSet<String> set = new HashSet<>();
int N = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
set.add(st.nextToken());
}
int M = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
for(int i=0; i<M; i++) {
String card = st.nextToken();
if(set.contains(card)) sb.append("1" + " ");
else sb.append("0" + " ");
}
bw.write(sb.toString()+"\n");
bw.flush();
bw.close();
br.close();
}
}
작성코드 - 이분탐색 활용
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import java.io.*;
import java.util.*;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
Arrays.sort(arr);
int M = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
for(int i=0; i<M; i++) {
int card = Integer.parseInt(st.nextToken());
if(Arrays.binarySearch(arr, card) >= 0) sb.append("1").append(" ");
else sb.append("0").append(" ");
}
bw.write(sb.toString()+"\n");
bw.flush();
bw.close();
br.close();
}
}
회고
- 이분탐색에 대한 공부가 되어 있지 않아 Arrays.binarySearch() 메서드를 처음 사용해보았는데, 왜 정렬된 배열이 요구되는지 알아보고, 라이브러리 사용이 아닌 직접 구현해보는 공부도 진행해야겠다.
