[Java] 백준(실버-4) 1920번 - 수 찾기

문제 풀이

---

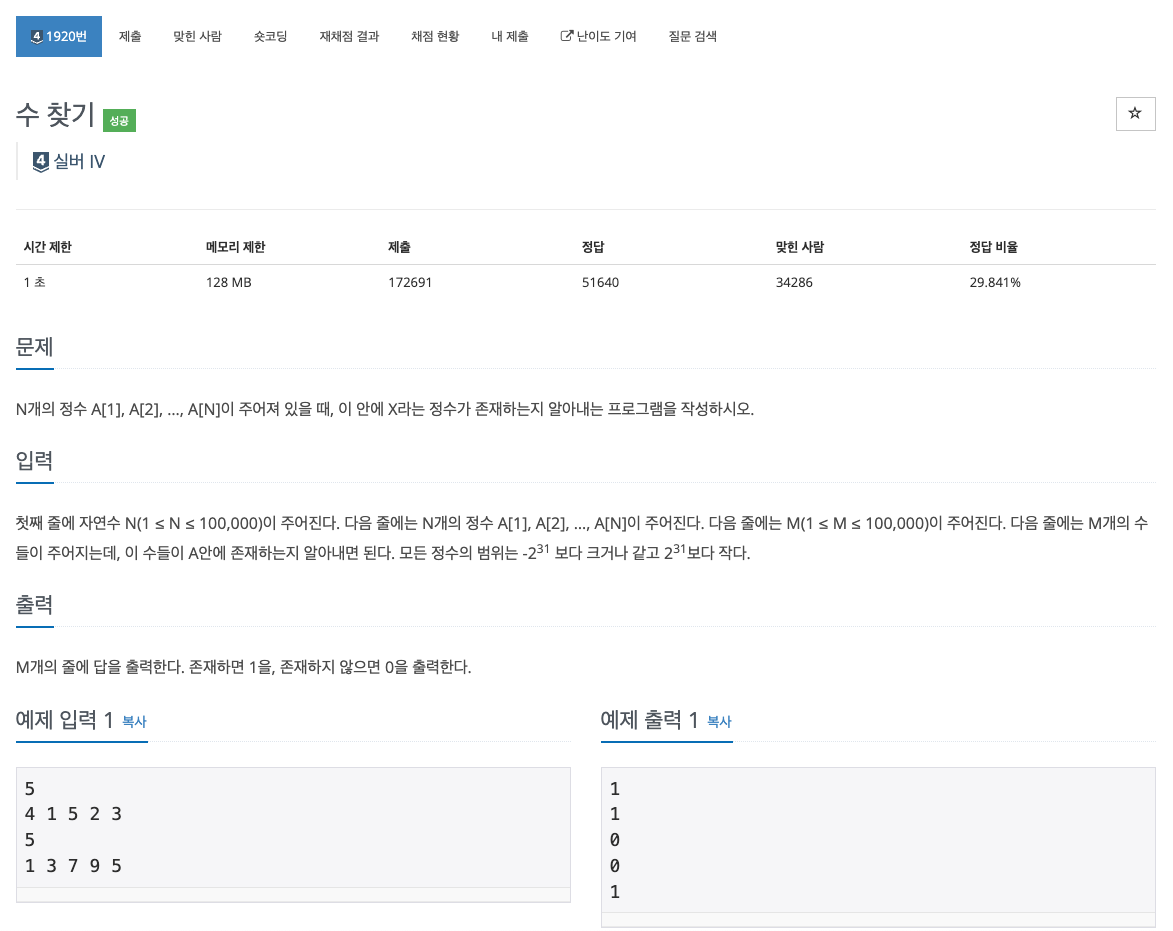
이번 문제는 시간 제한이 1초이고, 주어지는 정수의 범위가 2의 31승 정도로 굉장히 크다.
그렇기에 중첩반복문을 사용하게 되면 시간 초과가 발생할 것이기에 O(lonN)의 시간복잡도를 가지는 이분 탐색을 활용해야 한다.

이분(이진)탐색이란?
이진 탐색(이분 탐색) 알고리즘은 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법이다.
변수 3개(start, end, mid)를 사용하여 탐색한다. 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는 것이 이진 탐색의 과정이다.

아이디어 도출

• N개의 수들을 배열에 저장한 뒤 해당 배열을 오름차순으로 정렬한다.
• M개의 수별로 N개의 수들을 저장한 배열에 이분 탐색을 하여 M개의 수들 중 해당 배열에 포함된 수가 있는지 검증한다.

말 그대로 이분 탐색을 위해 배열을 정렬한 뒤 정렬한 배열에서 M개의 수들에 대한 이분 탐색을 진행하면 된다.
바로 코드를 작성해보자.

int N = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine());
int[] A = new int[N]; 
for(int i=0; i<A.length; i++) {
    A[i] = Integer.parseInt(st.nextToken());
}

N을 입력받고 N개의 수들을 배열에 저장한다.

int M = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());

Arrays.sort(A);

M을 입력받은 후 이분 탐색을 위해 앞에서 N개의 수들을 저장한 배열을 정렬한다.

이분 탐색을 위해서 왜 배열을 정렬해야 하나?
이진 탐색은 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘이기 때문이다.

for(int i=0; i<M; i++) {
    int num = Integer.parseInt(st.nextToken());
    int res = 0;
    if(Arrays.binarySearch(A, num) >= 0) res = 1;
    bw.write(res+"\n");
}

M개의 수를 입력받으며 Arrays에서 제공하는 binarySearch() 메서드를 활용해 A배열에 포함되는지 이분 탐색을 진행한다.
해당 메서드의 반환값이 0보다 크거나 같다면 M번째 수는 A배열에 포함되었다는 뜻이기에 “1”을 출력하면 되고,
음수가 나왔다면 A배열에 없는 수이기에 “0”을 출력하면 된다.

작성코드

---

import java.io.*;
import java.util.*;

class Main {
    public static void main(String[] args) throws IOException {
        
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int N = Integer.parseInt(br.readLine());
        StringTokenizer st = new StringTokenizer(br.readLine());
        int[] A = new int[N]; 
        for(int i=0; i<A.length; i++) {
            A[i] = Integer.parseInt(st.nextToken());
        }

        int M = Integer.parseInt(br.readLine());
        st = new StringTokenizer(br.readLine());
        
        Arrays.sort(A);

        for(int i=0; i<M; i++) {
            int num = Integer.parseInt(st.nextToken());
            int res = 0;
            if(Arrays.binarySearch(A, num) >= 0) res = 1;
            bw.write(res+"\n");
        }

        bw.flush();
        bw.close();
        br.close();
    }
}

회고

• O(logN)의 시간복잡도를 가지는 이분(이진)탐색 알고리즘을 활용하는데, Arrays 패키지에 존재하는 binarySearch 메서드를 통해 손쉽게 솔루션 코드를 작성할 수 있었다.

출처

• 해당 문제의 저작권은 문제를 만든이에게 있으며 자세한 내용은 문제 링크에서 참조바랍니다.