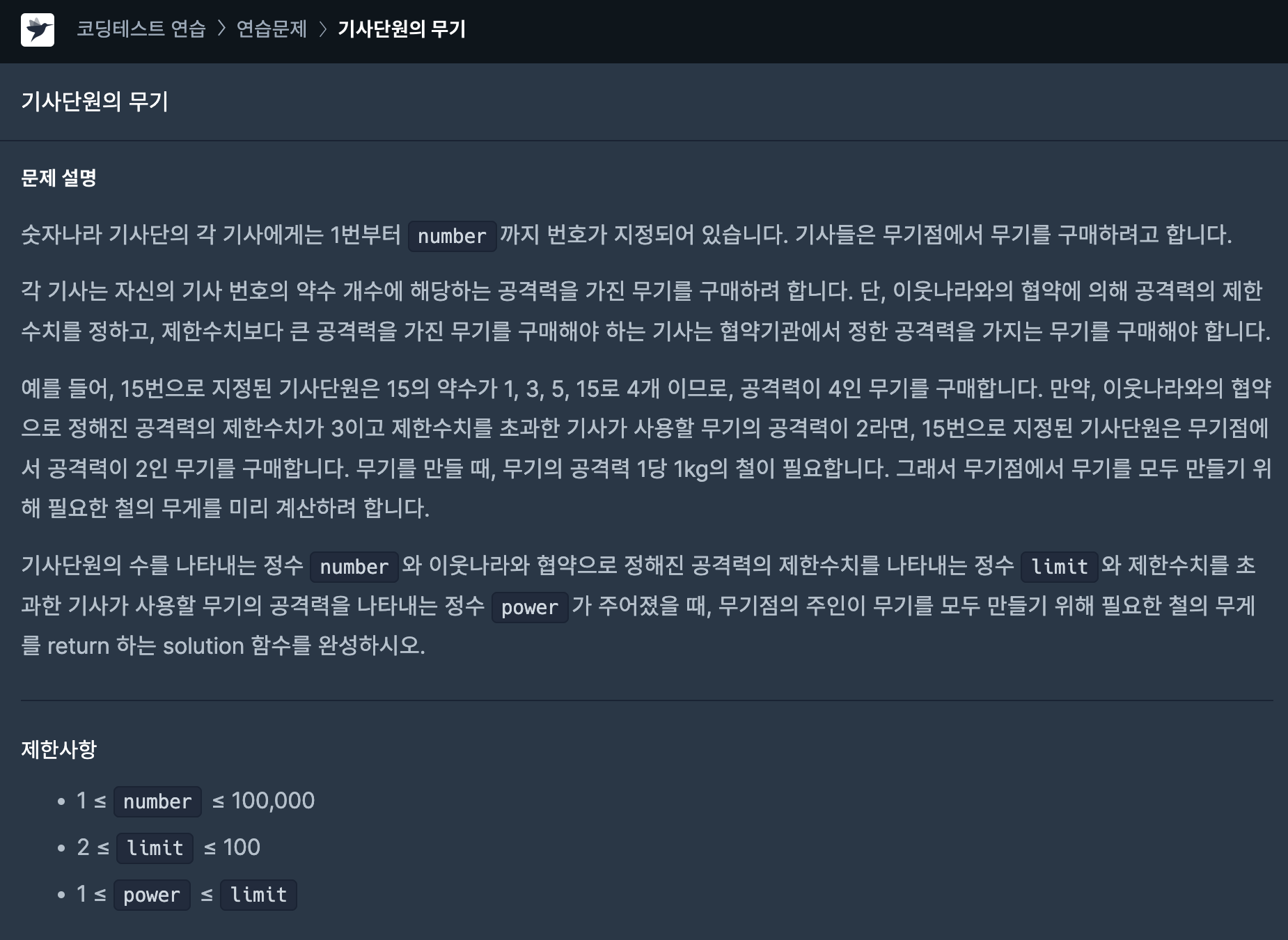
[Java] 프로그래머스(level-1) - 기사단원의 무기

문제 풀이

---

이번 기사단원의 무기 문제는 전반적인 구현까지의 과정은 단순하나 중간에 필요한 약수 개수를 구하는 알고리즘을 잘 구성해야 한다.

아이디어 도출

• 주어진 number 만큼 1부터 number까지 배열로 만든다.
• 위에서 만든 배열을 순회하면서 각 요소마다 약수의 개수를 구하고 이를 공격력으로 칭한 변수에 담는다.
  • 약수의 개수를 구하는 로직을 별도의 함수에서 수행한다.
• 구한 공격력(약수의 개수)가 limit보다 크다면, power로 대체한다.
• 마지막으로 모든 공격력의 누적합을 구하면 요구하는 철의 무게가 된다.

아이디어 자체는 간단하니 바로 코드를 작성해보자.

int answer = 0;
int[] knights = new int[number];

for(int i=0; i<number; i++) {
    knights[i] = i+1;
}

먼저 모든 기사단원의 공격력을 합해 철의무게를 반환할 answer 변수와 주어진 number 만큼의 크기를 가질 knights 배열을 선언한다.
그리고 1부터 number까지의 수로 knights 배열을 초기화한다.

for(int i=0; i<knights.length; i++) {
    int atk = divisor(knights[i]);
    if(atk > limit) atk = power;
    answer += atk;
}

그리고 knights 배열을 순회하면서 각 요소마다 atk이라는 변수에 약수의 개수를 구해서 담는다.
이 때, 구한 atk가 limit보다 크다면 power로 대체시키면 된다.

이렇게 구한 atk들의 누적합을 구한다면 요구하는 철의 무게를 구할 수 있다.
그런데 아이디어 자체는 크게 문제가 없어보였지만, 약수의 개수를 구할 때 시간초과 문제가 발생하게 되었다.

일반적으로 약수의 개수 구하기

알고보니 아무 생각없이 작성했던 약수를 구하는 로직 자체가 문제였다.
number의 수가 커질수록 그만큼 반복문이 돌아야 하기 때문에 시간적으로 매우 비효율적이라는 것을 알 수 있었다.

// 일반적인 약수를 구하는 방법
for(int i = 1; i <= n; i++){
    if(n % i == 0) cnt++;
}

문제의 제한사항을 살펴보니 다음과 같았다.

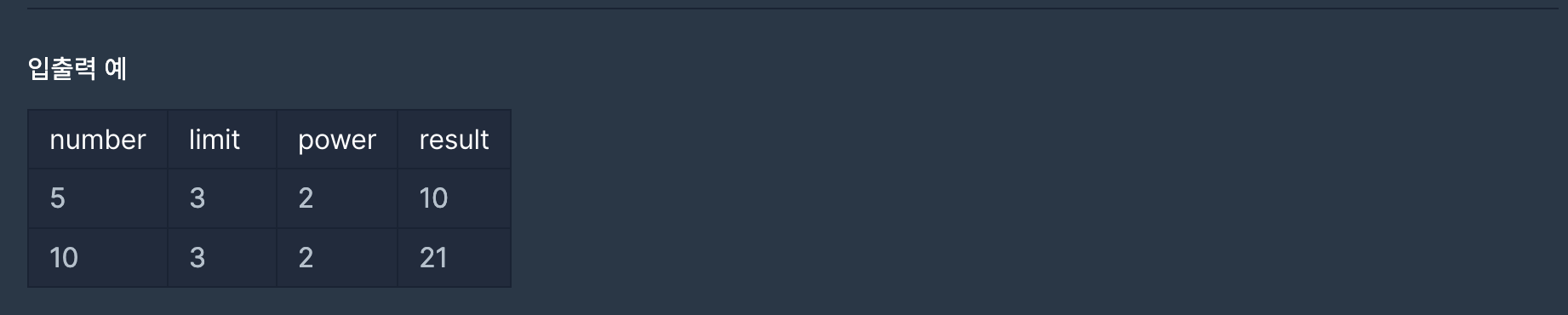
• 1 ≤ number ≤ 100,000
• 2 ≤ limit ≤ 100
• 1 ≤ power ≤ limit

number가 최대 십만까지 주어질 수 있기에 그만큼 배열의 길이가 늘어날테니 이를 고려하기 위해서는 결국 약수를 구하는 로직의 시간을 줄여야 한다.

약수의 개수를 보다 효율적으로 구하기

앞에서 약수를 구할 때 발생한 시간초과 해결을 위해 약수 개수 구하는 알고리즘 수정해야 했다.

만약 n의 약수가 1일 때 다른 약수는 n/1이 되므로 다른 하나의 약수는 number가 된다.
이 때, n의 약수 중 하나를 i라고 한다면, 다른 약수는 n/i 가 되므로 하나의 약수를 알면 다른 하나의 약수의 존재가 보장된다.

이를 코드로 표현하면 다음과 같다.

for(int i=1; i * i <= n; i++) {
    if(i * i == n) cnt++;
    else if(n % i == 0) cnt+=2;
}

우선, for 루프에서 i는 1부터 n의 제곱근까지 증가시킨다. 그 이유는 n의 제곱근 이후의 값에서는 n을 나누어 떨어지는 수가 나오지 않기 때문이다.
예를 들자면, n이 16이라면 4 이후의 값에서는 16을 나누어 떨어지게 하는 수가 없는 것과 같다.

다음으로, i * i 가 n과 같으면, i는 n의 약수이기 때문에 cnt 변수를 1만큼 증가시킨다.
그런데, 만약 i * i 가 n과 같지 않으면서 n을 i로 나누어 떨어지게 하는 경우, i와 n/i 둘 다 n의 약수인 것으로 보고 cnt 변수를 2만큼 증가시키면 된다.

이처럼 약수의 개수를 구하는 알고리즘 n의 제곱근을 황용하여 효율적으로 수정할 수 있었고, 정상적으로 테스트케이스를 모두 통과할 수 있었다.

작성 코드

---

import java.util.*;

class Solution {
    public int solution(int number, int limit, int power) {

        int answer = 0;
        int[] knights = new int[number];

        for(int i=0; i<number; i++) {
            knights[i] = i+1;
        }

        for(int i=0; i<knights.length; i++) {
            int atk = divisor(knights[i]);
            if(atk > limit) atk = power;
            answer += atk;
        }
        
        return answer;
    }
    
    public static int divisor(int n) {
        int cnt = 0;
        for(int i=1; i*i<=n; i++) {
            if(i * i == n) cnt++;
            else if(n % i == 0) cnt+=2;
        }
        return cnt;
    }

    public static void main(String[] args){
        Solution sol = new Solution();
        int number = 10;
        int limit = 3;
        int power = 2;
        sol.solution(number, limit, power);
    }
}

회고

• 약수의 개수를 구하는 알고리즘에 대해서 다시 한번 생각해보고 고민하여 약수를 구할 수의 제곱근을 황용하여 보다 효율적인 방법으로 약수의 개수를 구할 수 있었다.