[Java] 백준(골드-5) 2023번 - 신기한 소수
문제 풀이
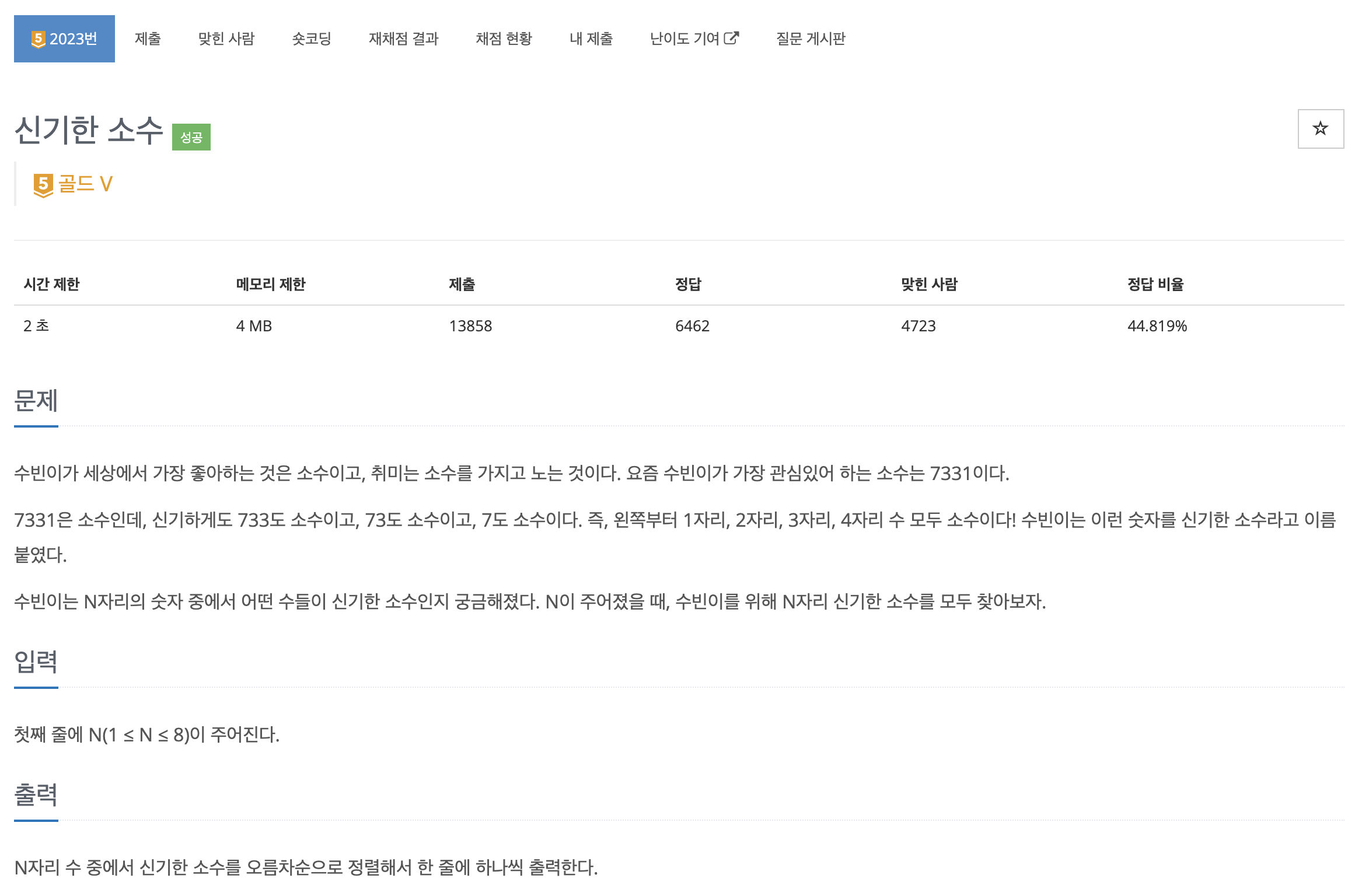
이번 신기한 소수 문제는 소수를 구하는 방법과 재귀를 잘 고려해야 한다.
소수를 판별하기 위해 제곱근까지 순회하는 방식을 이용하였고, 각 자리수별로 소수인지를 알아내기 위해서 재귀를 사용하였다.
에라토스테네스의 체

에라토스테네스의 체는 소수가 되는 수의 배수를 지우면 남은 건 소수가 된다.라는 원리의 알고리즘이라고 보면 된다.
그래서, 소수가 무엇인지 찾을 필요가 없으며 2부터 자기 자신을 제외한 배수를 지우면 된다.
에라토스테네스의 체를 이용한 소수 배열을 만들 경우 메모리 초과 발생
1
2
3
4
5
6
7
8
9
10
11
12
int N = Integer.parseInt(br.readLine());
int start = (int) Math.pow(10, N-1);
int end = (int) Math.pow(10, N) - 1;
boolean[] prime_arr = new boolean[end+1];
prime_arr[0] = prime_arr[1] = true;
for(int i=2; i<=Math.sqrt(end); i++) {
for(int j=i+i; j<prime_arr.length; j+=i) {
prime_arr[j] = true;
}
}
위처럼 에라토스네테스의 체를 이용해 소수 배열을 만들어 두고 문제를 풀려했으나 메모리 초과가 발생하였다.
그래서 문제 요구사항을 다시 살펴보았다.
- 시간 제한: 2초
- 메모리 제한: 4MB
이 문제는 메모리 제한이 4MB밖에 되지 않기 때문에 에라토스테네스의 체 알고리즘을 이용해서 배열에 소수 판별을 저장한 배열을 사용한다면 N이 8까지 주어질 수 있어, 천만 자리수까지 고려해야 하기에 메모리 초과가 발생하게 되었다고 판단하였다. 또한, 위 코드는 시간 복잡도가 O(NloglogN)으로, 지금처럼 n이 매우 큰 경우라면 시간초과가 추가적으로 발생할 우려가 있었다.
그래서 에라토스테네스의 체를 소수 배열을 만드는 것에 이용하는 것이 아니라 재귀함수를 이용해 모든 수를 탐색하며 소수 판별을 하는데 이용해야 한다.
문제 분석 및 아이디어 도출
일단 N은 1부터 8까지의 범윌를 가지고 있으며 1이면 1자리수, 2이면 2자리수 형식의 범위를 나타낸다. 또한, 이 문제의 핵심은 자릿수를 하나씩 붙여가는 과정에서 수 대부분을 쉽게 가지 칠 수 있다는 점이다.
- 몇 자리수가 됐든, 소수가 되려면 왼쪽부터 1자리 수가 소수여야만 한다. 즉 신기한 소수의 첫째 자리 수는 소수인
2,3,5,7중의 하나이고 이 경우에만 다음 자릿수를 붙여가면 된다.
첫째 자리 수부터 살펴보자.
소수인 2에 0~9까지 다음 자릿수를 붙여준다면 23과 29를 제외한 20,21,22,24,25,26,27,28 는 소수가 아니기 때문에 걸러낼 수 있다. 이렇게 소수가 아니라면 다음 자리수를 붙일 필요가 없다. 결국, 소수가 되는 23과 29의 경우에만 다음 자릿수를 붙여가면 된다.
주어진 예제와 같이 N이 4일 경우를 살펴보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// N = 4
// 1000 ~ 9999 까지 중에서 모든 신기한 소수를 출력해야 한다.
1
2 -> 소수
20
21
22
23 -> 소수
230
231
232
233 -> 소수
2330
2331
2332
2333 -> 신기한 소수(length = 4 = N)
...
...
24
25
26
27
28
29 -> 소수
3 -> 소수
30
...
4
5 -> 소수
50
...
6
7 -> 소수
70
...
8
9
2가 아닌 나머지 3,5,7의 경우에도 동일하게 진행하면 된다. 그렇게 이 과정을 반복하며 N의 자리까지 자릿수를 붙여가며 만들어진 수가 N만큼의 길이를 가졌을 때 그 수가 소수라면 앞에서 자리수 별로 소수 여부를 판별하고 지나왔기에 신기한 소수일 수밖에 없는 것이다.
위에서 짠 아이디어를 토대로 코드를 작성해보자.
1
2
3
4
class Main {
static int N;
...
}
먼저 입력받을 N을 재귀 메소드에서 사용하기 위해 static 키워드를 붙여서 Main 클래스의 모든 메소드에서 사용할 수 있도록 선언하였다.
1
2
3
4
5
6
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
recursion("");
br.close();
}
main 메소드에서는 N을 입력받고 recursion이라는 재귀메소드를 호출하였다.
1
2
3
4
5
6
7
8
9
10
11
12
// 재귀를 통해 N만큼 자리수를 붙여가기
public static void recursion(String str) {
if(str.length() == N) {
System.out.println(str);
return;
}
for(int i = 1; i <= 9; i++) {
if(isPrime(Integer.parseInt(str + i))) {
recursion(str + i);
}
}
}
recursion 재귀 메소드를 살펴보자.
str 변수에 ""과 같은 빈 문자열을 받아와서 실행되며, 1부터 9까지의 문자를 이 str 문자열 변수에 붙여가는데, str 변수에 1부터 9까지 붙여가면서 해당 문자열이 소수인지를 검증한다.
만약 소수라면 str+i 라는 수가 소수이기에 str+i라는 문자열을 파라미터로 함수를 재귀 호출한다. 이 과정을 반복하면서 str의 길이가 N만큼 채워졌다면 신기한 소수가 된 것이기에 출력하고 재귀를 종료한다.
1
2
3
4
5
6
7
8
9
// 에라토스테네스의 체로 소수 판별하기
public static boolean isPrime(int num) {
int sqrt = (int) Math.sqrt(num);
if (num == 1) return false;
for (int i=2; i<=sqrt; i++) {
if (num % i == 0) return false;
}
return true;
}
마지막으로 소수를 판별하는 로직이다. 앞서 말했듯 해당 범위 수의 제곱근까지만큼만 순회하면서 소수를 판별하도록 하였다. 1은 소수가 아니기에 false를 반환하고, 2부터 i의 제곱근까지 순회하면서 소수인 수를 걸러낸다.
이 떄, 여기서 i를 제곱근까지만 반복하는 이유는 i의 제곱이 n보다 크면, i와 n/i 중 하나는 반드시 n의 제곱근보다 작기 때문이다. 예를 들어, 121의 약수를 구하려면 1부터 11까지 모두 확인해야 하는데, 11보다 큰 약수는 이미 11보다 작은 약수를 통해 구할 수 있기 때문에 11까지만 확인하면 된다. 따라서, i를 제곱근까지만 반복하면, n의 제곱근보다 큰 약수는 확인할 필요가 없어지므로, 반복 횟수를 줄여 연산 속도를 향상시킬 수 있는 것이다.
작성코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
class Main {
static int N;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
recursion("");
br.close();
}
// 재귀를 통해 N만큼 자리수를 붙여가기
public static void recursion(String str) {
if(str.length() == N) {
System.out.println(str);
return;
}
for(int i = 1; i <= 9; i++) {
if(isPrime(Integer.parseInt(str + i))) {
recursion(str + i);
}
}
}
// 에라토스테네스의 체로 소수 판별하기
public static boolean isPrime(int num) {
int sqrt = (int) Math.sqrt(num);
if (num == 1) return false;
for (int i=2; i<=sqrt; i++) {
if (num % i == 0) return false;
}
return true;
}
}
회고
- 에라토스테네스의 체를 이용해 소수 배열을 만들어 사용하는 것이 아니라, 소수를 판별하기 위한 방법으로 사용해볼 수 있었다.
- 아직 공부가 더 필요하지만, 재귀함수를 이용해 깊이 우선 탐색인 DFS를 구현할 수 있었다.
출처
- 해당 문제의 저작권은 문제를 만든이에게 있으며 자세한 내용은 문제 링크에서 참조바랍니다.
