[Java] 백준(실버-3) 18310번 - 안테나
문제 풀이
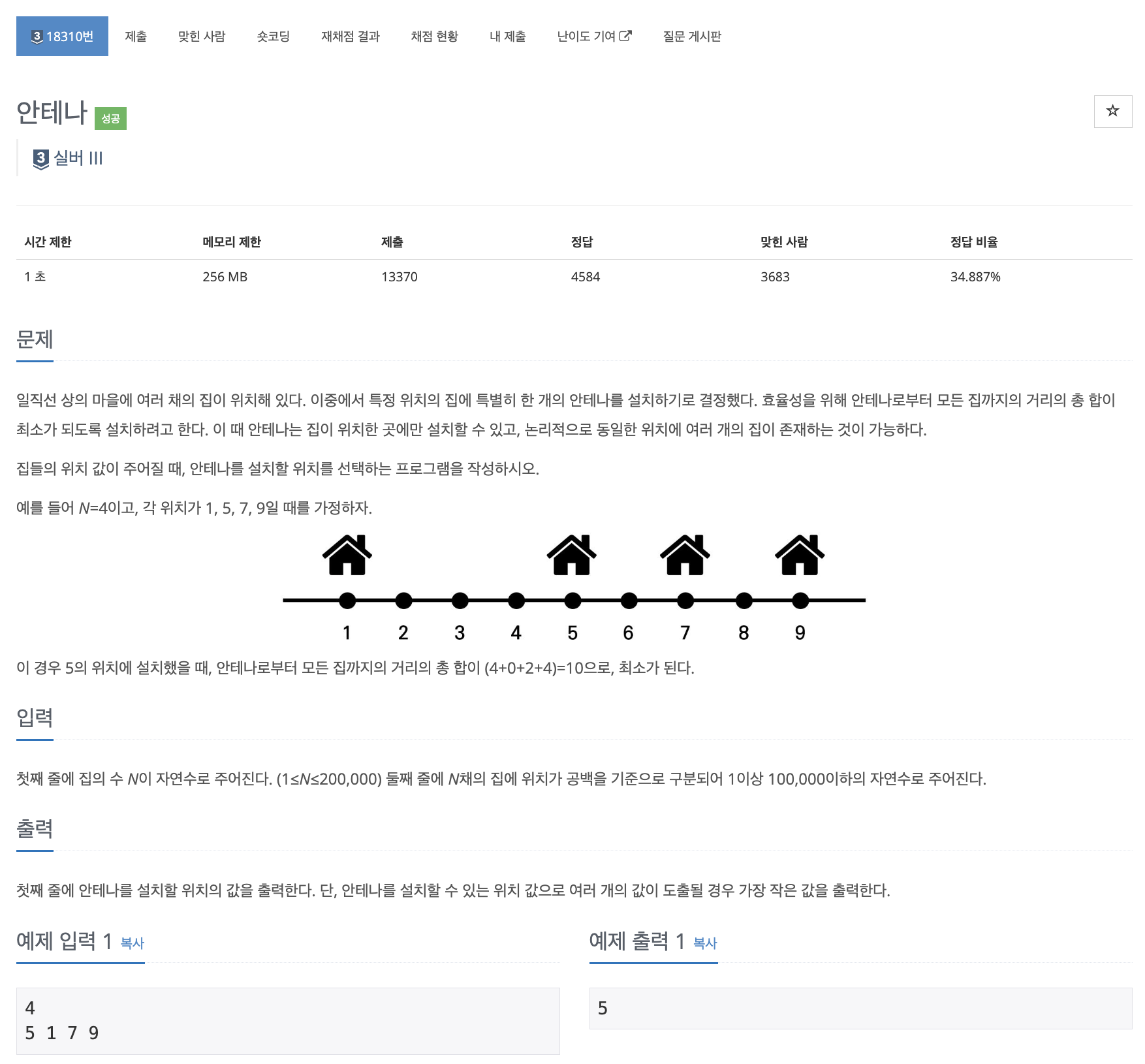
이번 문제는 그리디 알고리즘과 정렬을 알고 있다면 쉽게 풀 수 있는 문제이다.
그리디 알고리즘이란?
그리디 알고리즘(Greedy Algorithm)은 최적해를 구하는 데 사용되는 방법 중 하나이다. 가장 직관적인 알고리즘 설계 패러타임 중 하나이며, 매번 단계에서 선택할 때마다 가장 좋은 답을 선택하는 기법이다. 지금 선택한 것을 앞으로의 남은 선택에 영향을 끼칠지 고려하지 않는다는 전제이며, 전반적으로 적절한 결과를 도출하자는 알고리즘 기법이다. 항상 최적의 답을 구하는 것은 아니지만 어느정도 최적의 답에 근사한 결과를 빠르게 구할 수 있다는 장점이 있다. 특정 상황에서는 그리디 알고리즘이 최적의 답을 보장할 수도 있다.
문제 분석
처음엔 단순히 집들의 평균거리를 구해서 평균과 가장 가까운 집을 선택하면 될 것이라 생각했지만 아니었다.
1
2
N = 5
1 6 9 9 9
위 예제를 보면 평균을 구하면 6.8이므로 가장 가까운 건 6이지만, 6의 거리 차이의 합은 14이고 9의 거리의 차이는 실제로 11이기에 6이 아닌 9일 때 최소 거리의 합이 충족된다.
따라서 평균 값으로 구하면 안된다는 것을 알 수 있었다.
- 처음
1의 위치에 있을 때 차이의 합은29(0+5+8+8+8)이다. 2의 위치에 있다면26(1+4+7+7+7)이다.3의 위치라면23(2+3+6+6+6)이다.4의 위치라면20(3+2+5+5+5)이다.5의 위치라면17(4+1+4+4+4)이다.6의 위치라면14(5+0+3+3+3)이다.7의 위치에 있다면13(6+1+2+2+2)이다.8의 위치에 있다면12(7+2+1+1+1)이다.9의 위치라면11(8+3+0+0+0)이다.
즉,1부터 순회하면 현재 위치보다 좌측 지점의 수만큼 +N이 되고, 현재 위치보다 우측 지점의 수만큼 -M이 되는 식이다.
그런데 문제에서 요구하는 것은 집이 위치한 곳에만 안테나 설치가 가능하다. 고로 주어지는 집들의 번호가 여러개일 때 항상 중위값에 위치한 집에 안테나를 설치하는 것이 가장 적절하다.
아이디어 도출
이번 문제는 주어진 집들 중 모든 집까지의 거리의 합이 최소가 되는 집을 찾는 문제이기 때문에 결국 가운데에 위치한 집이 최적의 선택이 된다. 그 이유는, 모든 집까지의 거리의 합이 최소가 되어야 하므로 중간에 위치한 집이 다른 집들로부터의 거리가 가장 적기 때문이다.
즉, 정렬 후 중간에 위치한 값을 출력해주면 된다. 그런데 문제에서는 여러 개의 값이 도출될 경우 가장 작은 값을 원한다고 했으니 N이 짝수일 때와 홀수 일때 기준으로 나누어서 중간 값을 구하면 된다.
예를 들어 5개라면 3번째 값, 6개라면 3번째 값을 출력하면 되는데, 인덱스로 따지면 N/2-1 인덱스의 값을 출력해주면 된다.
- N이 홀수일 때: arr[N/2]
- N이 짝수일 떄: arr[N/2-1]
이제 코드를 작성해보자.
1
2
3
4
5
6
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
N을 입력받고 N만큼의 크기를 가지는 배열을 하나 선언하자. 그리고 N만큼 공백 기준으로 입력받으면서 배열에 집들의 위치를 저장한다.
1
2
3
Arrays.sort(arr);
if(N % 2 == 0) bw.write(arr[N/2-1]+"\n");
else bw.write(arr[N/2]+"\n");
배열의 중간 값을 찾기 위해서 오름차순 정렬을 먼저 진행한다.
그리고 N이 짝수라면 arr[N/2-1]로 중간값을 찾을 수 있고, 홀수라면 arr[N/2]로 중간값을 찾으면 된다.
따라서, 주어진 집들을 오름차순으로 정렬한 후, 중간에 위치한 집을 선택하면 최적의 선택이 되어 모든 집까지의 거리의 합이 최소가 된다.
위와 같이 그리디 알고리즘을 사용하여 이 문제를 해결하였다.
작성코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.StringTokenizer;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
// 오름차순 정렬을 실시하여 배열의 중위값을 반환해야합니다
Arrays.sort(arr);
// 중위값은 N이 짝수인지, 홀수인지에 따라 나뉘어지므로 이 부분을 구분하여 답을 출력해야합니다
if(N % 2 == 0) bw.write(arr[N/2-1]+"\n");
else bw.write(arr[N/2]+"\n");
bw.flush();
bw.close();
br.close();
}
}
회고
- 이 문제에서도 가운데에 위치한 집이 최적의 선택이기 때문에 매 순간 최적인 선택을 하는 알고리즘인 그리디 알고리즘을 활용할 수 있었다.
출처
- 해당 문제의 저작권은 문제를 만든이에게 있으며 자세한 내용은 문제 링크에서 참조바랍니다.
