[Java] 백준(실버-2) 18353번 - 병사 배치하기
문제 분석
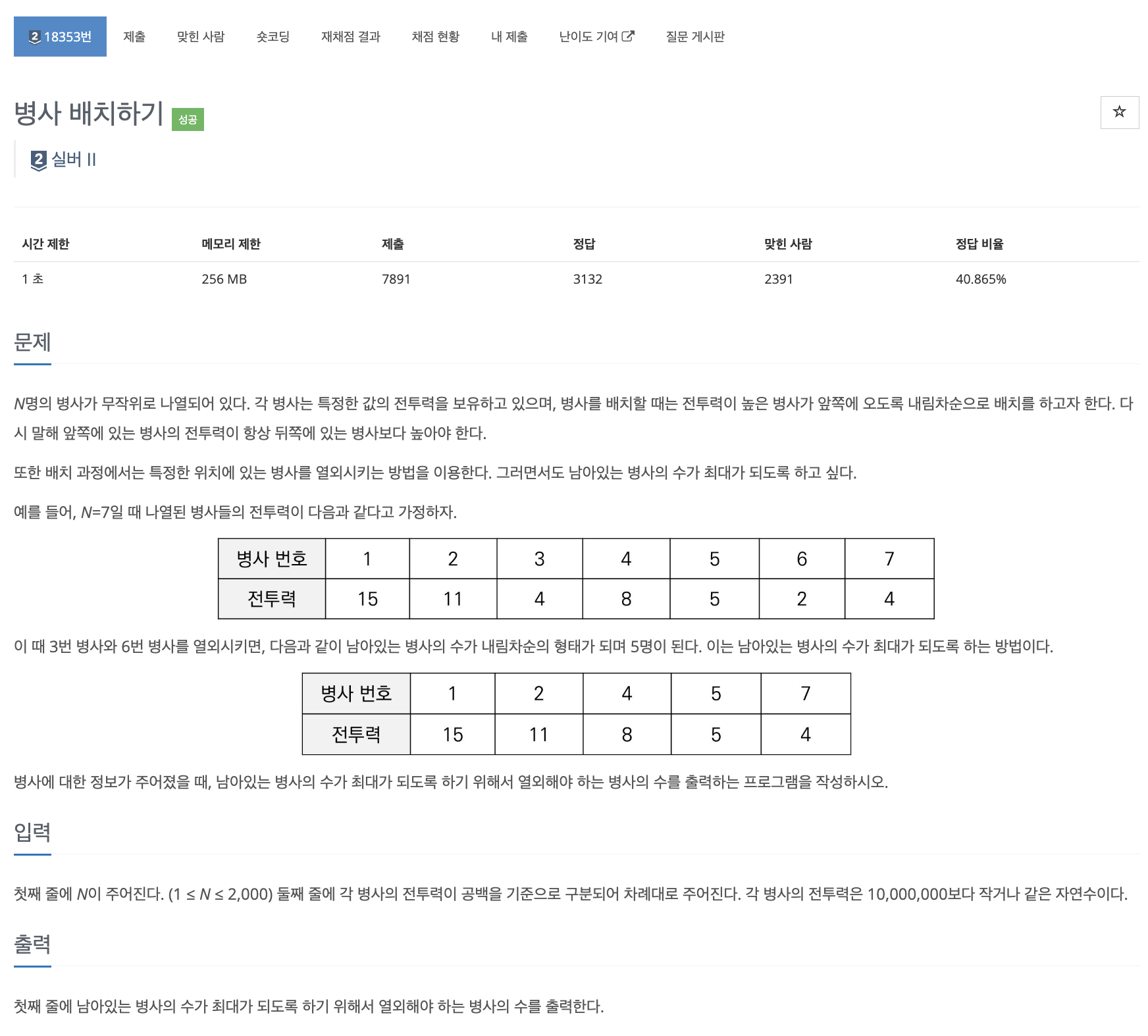
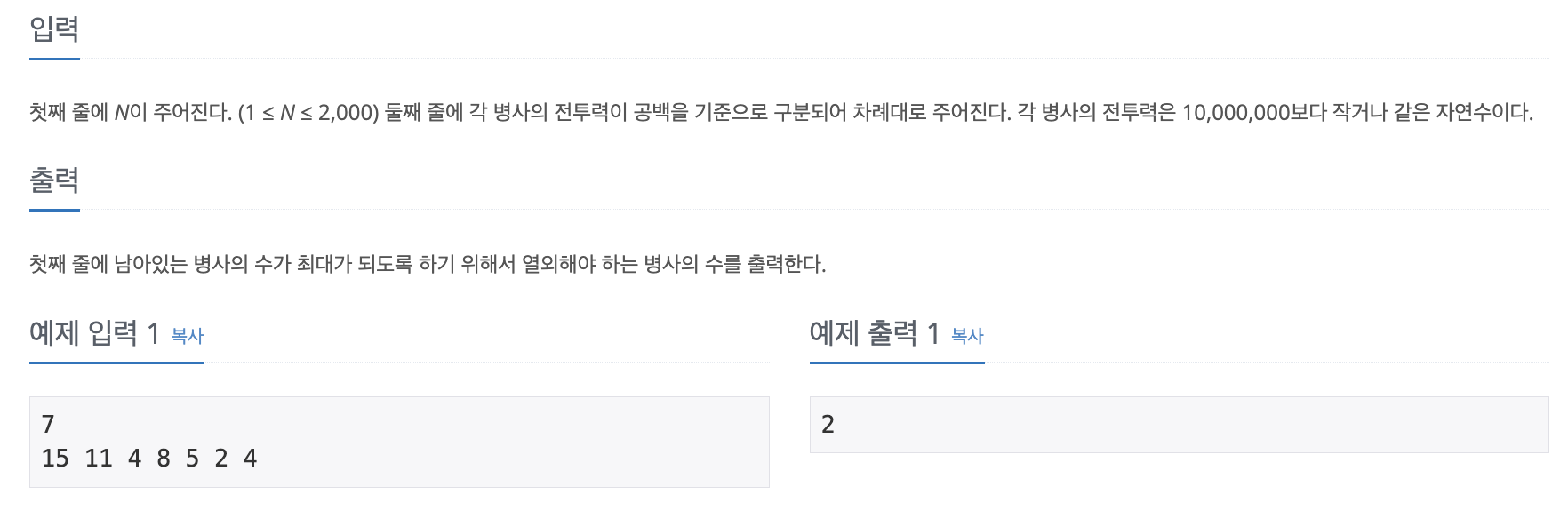
이번 문제는 내림차순으로 병사를 배치하기 위해서 내림차순 순서가 맞지 않는 병사들을 제외시켜야 한다.
이 때 LIS라는 최장 증가 부분 수열 알고리즘을 이용하여 정답을 구할 수 있다. 이 LIS를 구하기 위해 DP와 이분탐색 2가지 풀이 방법으로 문제를 풀어보겠다.
LIS란?
LIS(Longest Increasing Subsequenc)란 최장 증가 부분 수열이라고 한다. 즉 가장 긴 증가하는 부분 수열이라는 뜻이다.
LIS는 원소가 N개인 배열의 일부 원소를 골라내서 만든 부분 수열 중에서 각 원소가 이전 원소보다 크다는 조건을 만족하고, 그 길이가 최대인 부분 수열을 최장 증가 부분 수열이라고 한다. 바로 오름차순으로 증가하는 형태의 부분 수열이며, 해당 수열의 길이가 가장 긴 수열을 뜻한다.
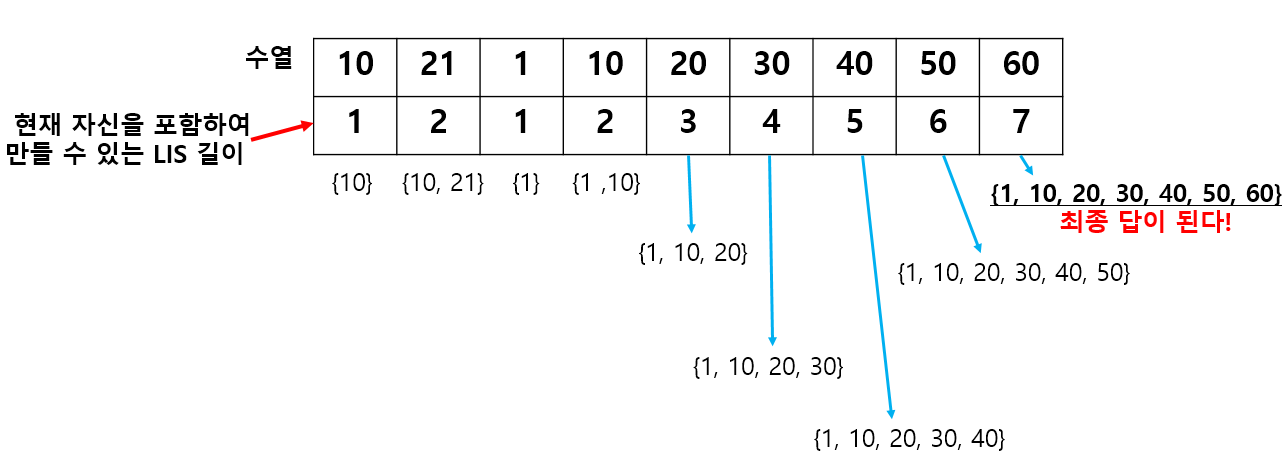
예를 들어, {10, 21, 1, 10, 20, 30, 40, 50, 60} 이라는 배열이 있을 경우, LIS는 {1, 10, 20, 30, 40, 50, 60}이다. {1, 10, 20}, {1, 10, 20, 30, 40}과 같이 증가하는 부분 수열은 많지만 그 중에서 가장 긴 수열이 LIS가 되기 때문에 {1, 10, 20, 30, 40, 50, 60}가 되는 것이다.
이러한 LIS, 즉 최장 증가 부분 수열의 길이를 구하는 것은 일반적으로 DP(동적계획법)을 이용한다.
DP(동적게획법)란?
DP란, 하나의 큰 문제를 작은 문제로 나누어 해결하는 기법을 의미한다. 특정한 알고리즘을 지칭하는 것이 아니라, 기법 그 자체를 의미한다. 같은 DP로 문제를 풀어도 다른 알고리즘을 이용할 수도 있다는 것이다.
DP의 2가지 조건
DP가 적용되기 위해서, 또는 문제풀이 기법이 DP라 부르기 위해서는 2가지 조건이 필요하다.
- 겹치는 소문제(Overlapping Subproblems)
- 최적 부분 구조(Optimal Substructure)
먼저 겹치는 소문제에 대해서 알아보자. 기본적으로 DP는 문제를 작은 문제로 나누고, 작은 문제의 결과를 재사용해서 원하는 결과를 도출하는 과정이다. 따라서 문제를 작은 문제를 나눴을 때 작은 문제들이 동일하게, 또는 비슷한 형태로 반복될 경우에 DP를 적용할 수 있다. 만약 문제를 나눌 순 있어도, 중복되는 부분이 없어 각 소문제의 결과를 재사용할 수 없다면 DP를 적용하기 어렵다.
다음은 최적 부분 구조이다. 소문제들의 최적 결과 값을 이용해 전체 문제의 최적 결과를 낼 수 있는 경우에 DP를 적용할 수 있다. 자세하게 설명해보자면, 소문제에서 구한 최적의 결과가 전체 문제에서도 적용되며 이는 변하지 않을 때만 DP를 사용할 수 있다는 것이다.
DP의 2가지 구현 방식
DP를 적용하는 단계에서 구현을 할 때, 보통 두 가지 방법이 있다. 각각 Top-Down방식과 Botton-Up방식이다.
Botton-Up방식은 말 그대로 초기조건을 기반으로 차곡차곡 데이터를 쌓아가 큰 문제의 결과를 도출하는 과정이다. 보통 반복문을 사용한다. 예를 들어 메모이제이션을 위한 배열 dp[]가 있었다면, dp[0] 부터 차례로 값을 채운다. Bottom-Up에 한하여 이러한 값 채우기를 본 떠 메모이제이션을 Tabulation이라 부르기도 한다.
Top-Down방식은 주로 재귀함수를 사용하며 dp[n]값을 찾기 위한 재귀 함수의 호출이 dp0 내려간 다음 결과들이 재귀 함수에 맞물리며 재활용되는 방식이다.
이번 문제는 Botton-Up방식을 활용하여 풀어보았다.
DP를 활용한 풀이 - Botton-Up
자, 이제 DP를 이용해 LIS의 길이를 구해서 제외해야할 병사의 수를 구하는 코드를 작성해보자.
1
2
static int[] seq;
static int[] dp;
주어진 병사의 전투력을 담을 int 배열 seq와 dp를 static 키워드로 선언하여 main 메소드 바깥에서도 사용할 수 있도록 선언하였다.
1
2
3
int N = Integer.parseInt(br.readLine());
seq = new int[N];
dp = new int[N];
첫번째 줄에서 병사의 수 N을 입력받은 후, seq 배열과 dp 배열을 N과 같은 크기로 초기화한다.
1
2
3
4
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
seq[i] = Integer.parseInt(st.nextToken());
}
두번째 줄에서 병사의 전투력을 공백 기준으로 입력받게 되는데 StringTokenizer를 이용해 seq 배열에 병사의 전투력을 입력순으로 저장한다.
1
2
3
4
5
6
7
8
9
10
11
12
int max = 0;
for(int i=0; i<N; i++) {
// 모든 부분 수열의 길이는 1이기에 먼저 1로 초기화
dp[i] = 1;
//
for(int j=0; j<i; j++) {
if(seq[j] > seq[i]) {
dp[i] = Math.max(dp[i], dp[j]+1);;
}
}
max = Math.max(max, dp[i]);
}
기본적인 LIS라면 오름차순 형식(최장 증가)의 부분 수열을 구해야 하겠지만 이번 병사 배치하기 문제에서는 내림차순으로 정렬된 형태(최장 감소)의 부분 수열들 중의 최대의 길이를 가지는 부분 수열을 구해야 한다.
그래서 0부터 N-1 만큼 탐색하면서 주어진 배열에서 인덱스(i)를 한 칸씩(+=1) 늘려가면서 확인한다.
그리고 중첩 for문에서 i보다 작은 인덱스(j)들을 하나씩 살펴 보면서 seq[j]가 seq[i]보다 큰 값이라면, dp[i] 를 새로 저장하면 된다.
여기서 dp[i]를 변경하는 값의 기준은 아래와 같다.
- i번째 인덱스에서 끝나는 최장 감소 부분 수열의 마지막에
seq[i]를 추가했을 때의 LIS 길이와, 추가하지 않고 기존의dp[i]값 둘 중에 더 큰 값(길이가 긴 값)으로dp[i]값을 변경하면 된다.
위와 같이 dp 배열을 채우면, dp 배열의 최댓값이 LIS의 길이가 되어 최댓값을 출력하면 된다. 이 때는, 바로 최장 감소 부분 수열을 구하기 위해 max라는 변수에 최대값을 저장하였다.
1
bw.write(N - max + "\n");
마지막으로 제외시킬 병사들의 수를 출력해야 한다. 결국 입력값 N에서 앞서 구한 max 값을 뺄셈한 값이 남아있는 병사들의 수가 된다.
이분 탐색읋 활용한 풀이 - 추가할 예정
앞에서 살펴본 DP를 통해 LIS를 구하는 방법의 시간복잡도는 O(n^2)가 되는데, 이는 굉장이 비효율적이다. 그래서 시간복잡도를 줄이기 위해 이분 탐색을 활용해보려 한다.
입력 값이 백만 개 정도만 되어도 O(n^2)의 알고리즘은 실행시간이 10초 이상 소요된다고 알려져 있다.
LIS의 형태를 유지하기 위해 주어진 배열의 인덱스를 하나씩 살펴보면서 그 숫자가 들어갈 위치를 이분탐색으로 탐색해서 넣는다. 이분탐색은 일반적으로 시간복잡도가 O(logn)으로 알려져 있으므로, 위의 문제를 O(blogs)의 시간복잡도로 해결할 수 있게 된다.
작성코드 - DP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
int[] seq = new int[N];
int[] dp = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
seq[i] = Integer.parseInt(st.nextToken());
}
int max = 0;
for(int i=0; i<N; i++) {
dp[i] = 1;
for(int j=0; j<i; j++) {
if(seq[j] > seq[i]) {
dp[i] = Math.max(dp[i], dp[j]+1);;
}
}
max = Math.max(max, dp[i]);
}
bw.write(N - max + "\n");
bw.flush();
bw.close();
br.close();
}
}
작성코드 - 이분 탐색
1
회고
- LIS라는 최장 증가 부분 수열을 구하는 알고리즘에 대해서 알아볼 수 있었다.
- DP를 풀 때 Botton-Up방식으로는 풀어보았지만, 재귀 호출을 주로 다루는 Top-down 방식으로도 풀어보아야 겠다.
-
dp 배열을 Integer 배열로 선언할 수 도 있었는데, 이유는 DP를 통해 반복을 하며 dp배열의 원소가 null일 때를 비교해야 하기 때문이다. 이 때, int 배열에서도 0으로 비교하면 되겠지만, Collections.max() 메소드로 LIS의 최대 길이를 구하기 위해 dp 배열을 List로 변환해야 하는데, int배열은 List로 변환되지 않기 때문이다.
- int 배열이 List로 변환되지 않는 이유는 int[] 배열은 기본 자료형(primitive type)의 배열이기에 Arrays.asList() 메소드를 통해 List로 변환할 수 없다. 이는 Arrays.asList() 메소드가 매개변수로 전달된 객체를 배열이 아닌 컬렉션(Collection) 형태로 반환하기 때문이다.
출처
- 해당 문제의 저작권은 문제를 만든이에게 있으며 자세한 내용은 문제 링크에서 참조바랍니다.
- LIS 이미지 출처
