[Java] 프로그래머스(level-2) - N개의 최소공배수

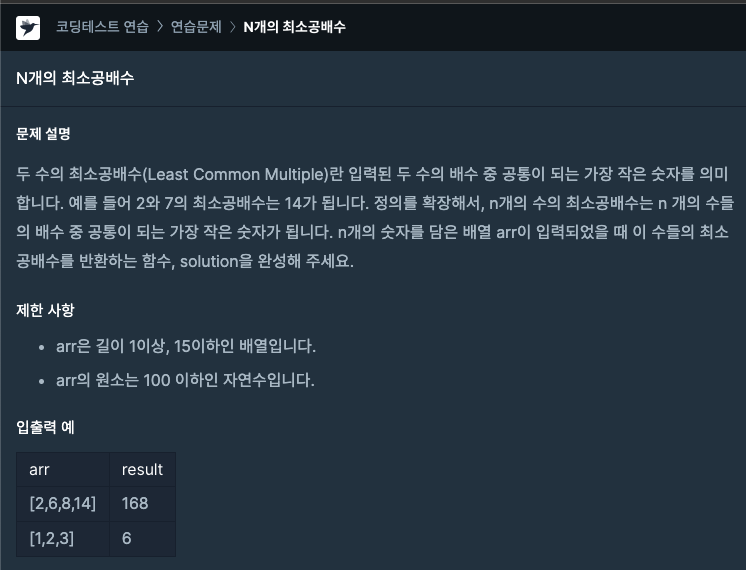
입출력 예시

Input-1
[2, 6, 8, 14]
Output-1
168

Input-2
[1, 2, 3]
Output-2
6

문제 풀이

문제의 핵심은 앞의 두 수를 가지고 구한 최소공배수를 가지고 다음 수와의 최소공배수를 구하는 방식으로 구해나가야 한다는 것이다.

먼저 최소공배수의 경우 두 수의 곱을 두수의 최대공약수로 나누면 된다.
최대공약수의 경우는 유클리드 호제법 함수를 통해 구하였다.

public static int gcd(int bn, int sn) { // 유클리드 호제법을 통해 최대공약수 찾기
    int r = bn % sn;
    if(r == 0) return sn;
    else return gcd(sn, r);
}

다음으로 N번째까지의 최소공배수를 구하기 위해 아래의 작업을 반복해야 한다.

• (이전 최소 공배수 * 다음 수) / GCD(이전 최소 공배수, 다음 수)

Arrays.sort(arr);
int answer = arr[0];
for(int i=1; i<arr.length; i++) {
    answer = (answer * arr[i]) / gcd(answer, arr[i]);
}

위 코드는 최소공배수를 구해나가는 과정을 작성한 것이다.
첫번째 수의 값을 answer에 담아서 반복문 내에서 첫번째 수를 대입한 후에는 구해진 최소공배수가 answer에 담겨져 위의 작업을 이행할 수 있게 된다.

arr [2, 6, 8, 14]

i = 1 //6일 때
    answer = arr[0] = 2
    gcd = (2,6) = 2
    answer = (2*6)/2 = 6

i = 2 //8일 때
    answer = 6
    gcd = (6,8) = 2
    answer = (6*8)/2 = 24

i = 3 //14일 때
    answer = 24
    gcd = (24,14) = 2
    answer = (24*14)/2 = 168

작성 코드

import java.util.*;

class Solution {
    public static void main(String[] args) {        
        int[] arr = {2,6,8,14};
        // int[] arr = {1,2,3};
        long start = System.currentTimeMillis();
        solution(arr);
        long end = System.currentTimeMillis();
        System.out.println("\n수행시간 = " + (end-start));
    }
    
    public static int solution(int[] arr) {
        Arrays.sort(arr);
        int answer = arr[0];
        for(int i=1; i<arr.length; i++) {
            answer = (answer * arr[i]) / gcd(answer, arr[i]);
        }
        return answer;
    }
    
    public static int gcd(int bn, int sn) { // 유클리드 호제법을 통해 최대공약수 찾기
        int r = bn % sn;
        if(r == 0) return sn;
        else return gcd(sn, r);
    }
}

회고

• 이전에 두수의 최대공약수와 최소공배수를 구하는 문제를 풀어보았기에 쉽게 문제풀이에 접근할 수 있었다.