[Java] 프로그래머스(level-1) - 크레인 인형뽑기 게임
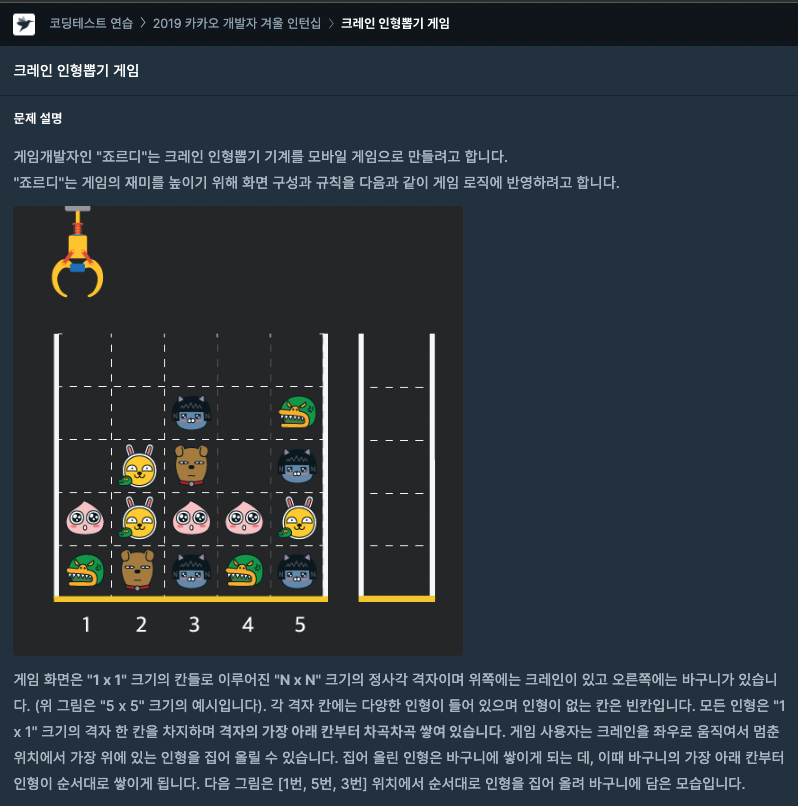
상세한 문제 내용은 여기에서 확인 바랍니다.
입출력 예시
Input
board = [[0,0,0,0,0],[0,0,1,0,3],[0,2,5,0,1],[4,2,4,4,2],[3,5,1,3,1]]
moves = [1,5,3,5,1,2,1,4]
Output
4
문제 풀이
문제 풀이를 위해 다음과 같은 아이디어를 도출하였다.
- 주어진 크레인 2차원 배열을 그대로 쓰는 것보단 인형뽑기를 하기 쉽도록 2차원 배열을 회전하여 활용하자.
- 인형뽑기하여 담는 바구니는 스택을 활용하여 구현하자.
2차원 배열 회전하기
먼저 주어진 board 2차원 배열을 크레인에서 뽑기 쉽게 회전해야 한다.
내가 생각한 회전 방법은 우측으로 90도를 회전하고 뒤집는 것이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 주어진 board 2차원 배열
0 0 0 0 0
0 0 1 0 3
0 2 5 0 1
4 2 4 4 2
3 5 1 3 1
// 우측으로 90도 회전 후
0 3 1 2 1
0 0 0 4 3
0 1 5 4 1
0 0 2 2 5
0 0 0 4 3
// 앞, 뒤 뒤집기
0 0 0 4 3
0 0 2 2 5
0 1 5 4 1
0 0 0 4 3
0 3 1 2 1
위 내용을 코드로 작성해보자.
1
2
3
4
5
6
for(int i=0; i<board.length; i++) {
for(int j=0; j<board[i].length; j++) {
new_board[i][j] = board[j][board.length-i-1]; // 우측으로 90도 회전
}
}
Collections.reverse(Arrays.asList(new_board)); // 2차원 배열의 순서 뒤집기
작성하고 나서 생각해보니, 우측으로 90도 회전하고 뒤집지 않고 한번에 왼쪽으로 90도 회원하는 코드를 작성하고 싶어 다시 고쳤다.
1
2
3
4
5
for(int i=0; i<board.length; i++) {
for(int j=0; j<board[i].length; j++) {
new_board[board[i].length-i-1][j] = board[j][board.length-i-1]; // 우측으로 90도 회전
}
}
위 코드와 같이 우측으로 90도 뒤집은 상태에서 인덱스를 뒤집어서 집어넣을 수 있도록 하니, 깔끔하게 해결되었다.
1
2
3
4
5
6
7
8
9
10
11
12
0 0 0 0 0
0 0 1 0 3
0 2 5 0 1
4 2 4 4 2
3 5 1 3 1
// 왼쪽으로 90도 회전
0 0 0 4 3
0 0 2 2 5
0 1 5 4 1
0 0 0 4 3
0 3 1 2 1
인형뽑기 게임 구현하기
이제 인형뽑기 할 수 있는 크레인 배열을 구했으니 실제로 인형뽑기하여 바구니에 쌓도록 해야하는데,
크레인 작동위치 배열 moves 만큼 반복하며 moves에 담긴 원소별로 크레인 위치마다 인형을 뽑아야 한다.
- 3중 반복문을 활용해 크레인 작동 위치(moves)별로 반복하며 크레인 배열(new_board)에서 0이 아닌 인형을 뽑는다.
- 뽑은 인형의 위치를 0으로 변경한다.
- 인형을 뽑아 바구니(스택)에 쌓는다.
- 뽑은 인형과 바구니에 맨 위 인형과 같다면 연속으로 인형을 뽑은 것이기에 터뜨린다.(스택에서 맨 위 인형 제거)
위 로직을 코드로 작성해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for(int i=0; i<moves.length; i++) {
for(int j=0; j<new_board.length; j++) {
for(int k=0; k<new_board[j].length; k++) {
if((moves[i]-1) == j && new_board[j][k] != 0) {
if(!result.empty() && result.peek()==new_board[j][k]) {
result.pop();
answer += 2;
}
else result.push(new_board[j][k]);
new_board[j][k] = 0;
break;
}
}
}
}
조금 복잡해보이지만 간단히 정리하자면,
두번째 인형을 뽑을 때부터 연속된 인형을 뽑았을 경우 스택에 쌓지 않고 제거하여 연속으로 뽑은 인형을 검증할 수 있다.
작성 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import java.util.*;
class Solution {
public static void main(String[] args) {
int[][] board = {{0,0,0,0,0},{0,0,1,0,3},{0,2,5,0,1},{4,2,4,4,2},{3,5,1,3,1}};
int[] moves = {1,5,3,5,1,2,1,4};
// int[][] board = {{0,0,0,0,0},{0,0,0,1,3},{3,1,5,4,2},{1,2,3,4,5},{3,2,1,4,5}};
// int[] moves = {1,5,4,2,3};
long start = System.currentTimeMillis();
solution(board, moves);
long end = System.currentTimeMillis();
System.out.println("\n수행시간 = " + (end-start));
}
public static int solution(int[][] board, int[] moves) {
int answer = 0;
int[][] new_board = new int[board.length][board.length];
Stack<Integer> result = new Stack<>();
for(int i=0; i<board.length; i++) {
for(int j=0; j<board[i].length; j++) {
new_board[board[i].length-i-1][j] = board[j][board.length-i-1]; // 왼쪽으로 90도 회전 및 상,하 뒤집기
}
}
for(int i=0; i<moves.length; i++) {
for(int j=0; j<new_board.length; j++) {
for(int k=0; k<new_board[j].length; k++) {
if((moves[i]-1) == j && new_board[j][k] != 0) {
if(!result.empty() && result.peek()==new_board[j][k]) {
result.pop();
answer += 2;
}
else result.push(new_board[j][k]);
new_board[j][k] = 0;
break;
}
}
}
}
return answer;
}
}
회고
- 2차원 배열을 회전하는 과정에서 많이 헷갈리는 부분이 많았다. 배열 회전이나 뒤집기 활용도 꾸준히 복습해야 겠다.
- 스택을 본격적으로 활용하며 특정 순서별로 제거해야 했지만, 짝 맞추는 것으로 헷갈려 인형을 터뜨리는 로직 구현에 오랜 시간이 걸렸다..ㅠ
