lango

찍먹? 부먹?
난 부먹 개발자.

2 minute read



입출력 예시

Input-1
3
Output-1
2

Input-2
5
Output-2
5


문제 풀이

문제 풀이에 앞서 피보나치 수에 대해서 알아보자.

피보나치(Fibonnaci)란?
피보나치 수열은 0과 1로 시작하며, 앞의 두 수를 더해서 다음 수를 만들어 나가는 수열이다.
F(n) = F(n-1) + F(n-2) 라는 식으로 볼 수 있다.
EX) 1,1,2,3,5,8,13,12 …

피보나치 수열이 만들어지는 패턴을 알아보자. (0과 1로 시작할 경우)

  1. F(0) = 0
  2. F(1) = 1
  3. F(2) = F(1)+F(0) = 0+1 = 1
  4. F(3) = F(2)+F(1) = 1+1 = 2
  5. F(4) = F(3)+F(2) = 2+1 = 3
  6. F(5) = F(4)+F(3) = 3+2 = 5
    이하 생략 …

위와 같은 방식으로 n번째의 피보나치 수를 찾아야 한다.

재귀함수로 n번째 피보나치 수 찾기

먼저 재귀함수를 활용해 n번째 피보나치 수를 찾아보자.

1
2
3
4
5
6
7
8
9
10
11

public static int solution(int n) {
    int answer = 0;
    for(int i=0; i<=n; i++) {
        answer = fibo(i);
    }
    return answer;
}
public static int fibo(int n) {
    if(n <= 1) return n;
    else return fibo(n-1) + fibo(n-2);
}

위 코드를 보면 fino()라는 함수를 통해 0부터 n까지 순회하며 피보나치 수를 찾도록 하였다.

재귀함수 테스트케이스 실행결과

그런데, 테스트케이스 7~14번까지 시간 초과가 발생하였다.
살펴보니 n이 50 이상일 경우에 재귀 호출을 사용한다면 시간초과가 발생하는 것을 확인하였다.

반복문으로 n번째 피보나치 수 찾기

그렇다면 재귀함수 대신 for문을 활용해 첫번째부터 n번째까지 순서대로 피보나치 수를 구해야 한다.

1
2
3
4

int n1, n2, fibo;
n1 = 0;
n2 = 1;
fibo = 1;

먼저 0과 1로 첫번째 피보나치 수 1을 만들어야 하기에 n1에 0을, n2에 1을, fibo에 1을 초기화한다.

1
2
3
4
5

for(int i=1; i<n; i++) {
    fibo = (n1 + n2)
    n1 = n2;
    n2 = fibo;
}

그리고 반복문을 돌면서 fibo에 n1과 n2를 더한 값을 저장하고, n1을 n2 값으로, n2를 fibo 값으로 재조정한다.

1
2
3
4

i=1, fibo = 0+1 = 1, n1=1, n2=1
i=2, fibo = 1+1 = 2, n1=1, n2=1
i=3, fibo = 1+1 = 2, n1=1, n2=2
i=4, fibo = 1+2 = 3, n1=2, n2=3 //fibo=n1+n2=5

n이 5일 때 i는 1부터 4까지 순회하므로 fibo값에 n1과 n2을 더해 5를 구할 수 있다. 

1

int answer = fibo % 1234567;

그리고 문제 요구사항대로 구한 피보나치 수에 1234567로 나눈 나머지 값을 answer에 담아 반환하도록 하였다.

반복문 테스트케이스 실행결과

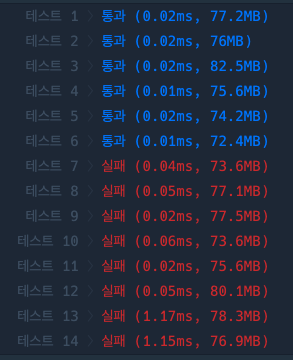
반복문을 통해 시간초과 문제는 해결됐지만, 여전히 테스트케이스 7~14번이 실패하였다.

오버플로우 발생

왜 실패하나 디버깅을 해보니, n이 47일 때부터 int형의 범위를 초과하여 오버플로우가 발생함을 확인하였다.
애초에 구해진 n번째 피보나치 수에만 1234567 나머지 연산을 수행하는 것이 잘못된 행위였다.
오버플로우를 해결하기 위해 반복문 내에서 N번째 피보나치 수를 구할 때마다 1234567 나머지연산을 수행하도록 변경하였다.

n번째 피보나치 수마다 나머지연산 수행

나머지연산을 반복문 단계별로 수행하도록 변경하니 int형 범위를 초과하지 않고 정상적으로 피보나치 수를 구할 수 있었다.

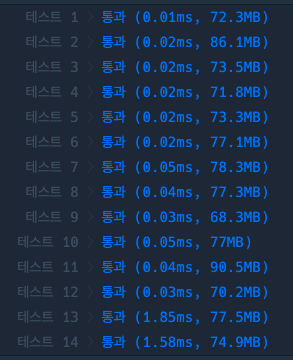
고친 코드로 테스트케이스를 채점해보니 모두 통과하였다.


작성 코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

import java.util.*;

class Solution {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        long start = System.currentTimeMillis();
        solution(n);
        long end = System.currentTimeMillis();
        System.out.println("\n수행시간 = " + (end-start));
    }
    public static int solution(int n) {
        int n1, n2, fibo;
        n1 = 0;
        n2 = 1;
        fibo = 1;
        
        for(int i=1; i<n; i++) {
            fibo = (n1 + n2) % 1234567;
            n1 = n2;
            n2 = fibo;
        }

        int answer = fibo;
        return answer;
    }
}

회고

  • 재귀함수의 경우 주어진 n이 클 경우에는 오랜 시간이 소요되기에 유의하며 사용해야함을 느꼈다.
  • 문제에서 구한 피보나치 수를 1234567로 나눈 나머지를 요구하는 것이 의아했지만, 결국 매 수마다 나머지연산을 통해 int형 범위를 보장하기 위함이라고 이해하였다.

You may also enjoy