[Java] 백준(실버-2) 9020번 - 골드바흐의 추측

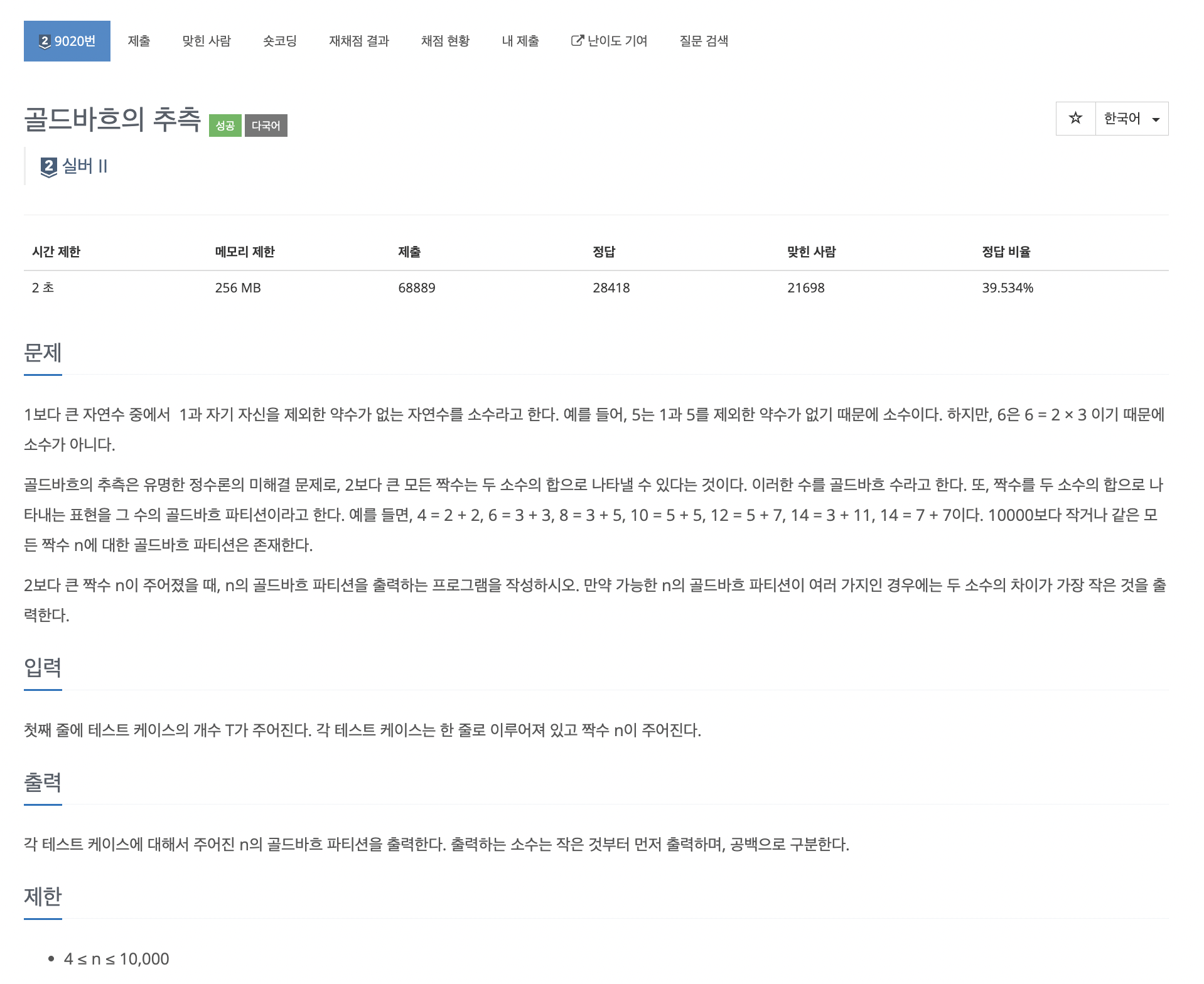
입출력 예시

Input

3
8
10
16

Output

3 5
5 5
5 11

문제 풀이

---

골드바흐의 추측이 뭔지 위키를 찾아보았다.

골드바흐의 추측이란?
이전부터 알려진 정수론의 미해결 문제로, 2보다 큰 모든 짝수는 두 개의 소수의 합으로 표시할 수 있다는 것이다.
이때 하나의 소수를 두 번 사용하는 것을 허용한다.

• 골드바흐의 강한 추측: 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다.
• 골드바흐의 약한 추측: 5보다 큰 모든 홀수는 세 소수의 합으로 나타낼 수 있다.

이 문제에서는 골드바흐 파티션, 즉 2보다 큰 모든 짝수를 두 소수의 합으로 나타내는 골드바흐의 강한 추측을 이용하여 두 소수를 구해야 한다.

두 소수를 구하기 위한 아이디어를 생각해보았다.

• n을 2로 나눈 수가 소수라면 n/2+n/2는 n이다.
• n을 2로 나눈 수가 소수가 아니라면 소수가 될 때까지 -1을 하거나 +1을 한다.

2보다 큰 짝수들의 예를 들어보면 금방 이해할 수 있다.

n=16 -> n/2=8(not prime number), 7(8-1)+9(8+1)=16
n=18 -> n/2=9(not prime number), 7(9-2)+11(9+2)=18
n=20 -> n/2=10(not prime number), 9(10-1)+11(10+1)=20
n=22 -> n/2=11(prime number), 11+11=22

그렇다면 코드를 작성해보자.

int T = Integer.parseInt(br.readLine());
for(int i=0; i<T; i++) {
    int n = Integer.parseInt(br.readLine());
    
    int small = n/2;
    int big = n/2;
    
    while(true) {
        if(isPrime(small)==2 && isPrime(big)==2) break;
        else {
            small-=1;
            big+=1;
        }
    }

    bw.write(small + " " + big + "\n");
}

테스트케이스 개수인 T를 입력받고, T만큼 n을 입력받는다.
두 소수를 가지고 n을 구해야 하니 먼저 n/2를 두 수(small, big)에 저장해두자.
그리고 small에는 -1을 big에는 +1을 하며 두 수가 소수가 될 때까지 반복하면 된다.

작성코드

import java.io.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
    
        int T = Integer.parseInt(br.readLine());

        for(int i=0; i<T; i++) {
            int n = Integer.parseInt(br.readLine());
            
            int small = n/2;
            int big = n/2;
            
            while(true) {
                if(isPrime(small)==2 && isPrime(big)==2) break;
                else {
                    small-=1;
                    big+=1;
                }
            }

            bw.write(small + " " + big + "\n");
        }
        bw.flush();
        bw.close();
        br.close();
    }

    public static int isPrime(int num) {
        int count = 0;
        for(int i = 1; i <= num; i++) {
            if(num % i == 0) count += 1;
            if(count >= 3) return count;
        }   
        return count;
    }
}

회고

• 두 소수의 합으로 2보다 큰 짝수를 구할 수 있는 골드바흐의 추측에 대해 공부할 수 있었다.