lango

찍먹? 부먹?
난 부먹 개발자.

2 minute read




문제 풀이

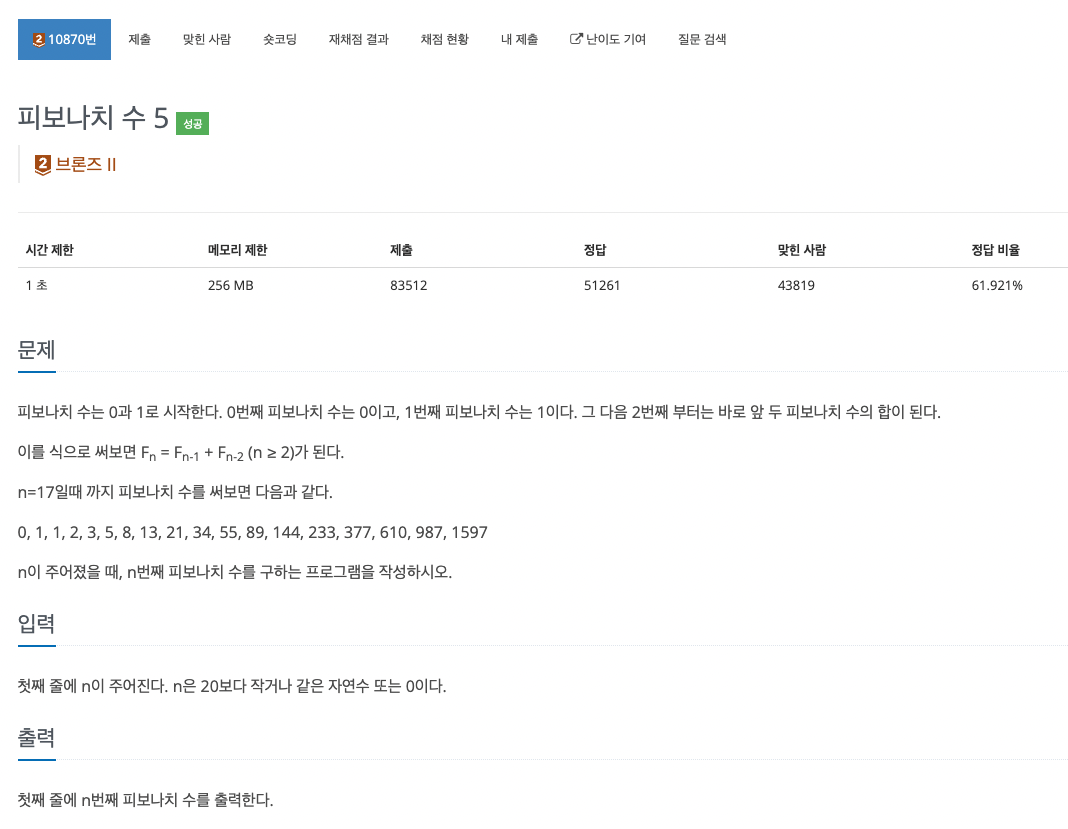
피보나치 수란 첫번째 항 0과 두번째 항 1부터 시작하여 앞 두수의 합으로 다음 수를 만들어 나가는 수열이다.
이번 피보나치 수 5 문제도 재귀함수 및 반복문을 활용하여 두가지 방식으로 풀어보았다.
피보나치 수에 대한 내용은 이전에 풀었던 피보나치 수 문제 에서 확인할수 있다.


재귀함수 활용하기

피보나치 수는 첫번째 항과 두번째 항이 0과 1로 고정이기에 N이 0과 1일 때 각각 0과 1을 반환하면 된다.
그러면 코드를 작성해보자.

1
2
3
4

public static int fibo(int n) {
    if(n <= 1) return n;
    return fibo(n-1) + fibo(n-2);
}

코드 자체는 단순하다. fibo 함수에서 n이 0이거나 1일 때 각각 0과 1을 반환하고, 그 외일 경우는 앞 두수의 합을 반환한다.



배열 및 반복문 활용하기

재귀함수 대신 배열과 반복문을 활용하여 피보나치 수를 구현해보자.
재귀함수를 이용한 방식과 비슷하게 앞 두수의 합을 배열 크기(N+1)만큼 원소에 더해가면 된다. 결국 배열의 마지막 원소가 구할 N번째 피보나치 수가 된다.
그럼 코드를 작성해보자.

1
2
3
4
5
6
7

int[] fibo_arr = new int[N+1];

for(int i=0; i<fibo_arr.length; i++) {
    if(i==0) fibo_arr[i] = 0; // 첫번째 항 0
    else if(i==1) fibo_arr[i] = 1; // 두번째 항 1
    else fibo_arr[i] = fibo_arr[i-1] + fibo_arr[i-2];
}

피보나치 수는 첫번째 항이 0부터 시작하기 때문에 배열의 크기도 N+1만큼 지정해주어야 한다.
첫번째 항과 두번째 항에 0과 1을 저장하고, 세번째 항 부터 앞 두수의 합을 저장해나가면 된다.
fibo_arr[N]번째 원소가 구하려는 N번째 피보나치 수이다.



작성코드

작성코드 - 재귀함수 활용

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

import java.io.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int N = Integer.parseInt(br.readLine());
        bw.write(fibo(N)+"\n");
        
        bw.flush();
        bw.close();
        br.close();
    }
    
    public static int fibo(int n) {
        if(n <= 1) return n;
        return fibo(n-1) + fibo(n-2);
    }
}

작성코드 - 배열 및 반복문 활용

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import java.io.*;
import java.util.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int N = Integer.parseInt(br.readLine());
        int[] fibo_arr = new int[N+1];

        for(int i=0; i<fibo_arr.length; i++) {
            if(i==0) fibo_arr[i] = 0; // 첫번째 항 0
            else if(i==1) fibo_arr[i] = 1; // 두번째 항 1
            else fibo_arr[i] = fibo_arr[i-1] + fibo_arr[i-2];
        }

        bw.write(fibo_arr[N]+"\n");
        
        bw.flush();
        bw.close();
        br.close();
    }
}

회고

  • 피보나치 수를 재귀함수를 통해 구하는 것 뿐 만 아니라 배열 및 반복문을 통해서도 구할 수 있었다.

You may also enjoy