[Java] 백준(브론즈-2) 25501번 - 재귀의 귀재

문제 풀이

---

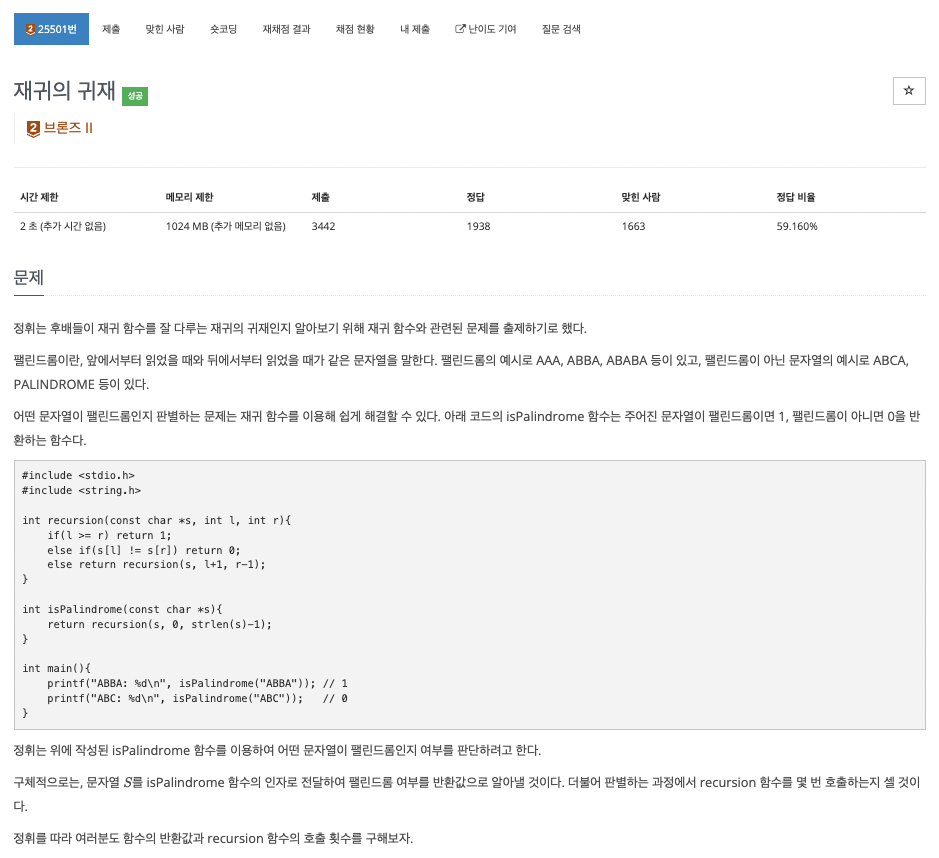
이 문제는 팰린드롬은 앞에서부터 읽었을 때, 뒤에서부터 읽었을 때가 같은 문자열인데, 주어진 테스트케이스마다 문자열이 팰린드롬인지 확인하고, 팰린드롬인지 판별하는 함수가 몇번 호출되었는지를 구해야 한다.
문제 힌트로 함수 코드를 제공하기 때문에 단순하게 팰린드롬 판별 함수인 recursion 함수의 호출 횟수만 구하면 된다.

recursion 함수 호출 횟수를 구하기 위해선 함수가 실행될 때마다 int형 변수를 증가시켜 반환하면 된다.
이 int형 변수를 배열에 담아 반환하는 방법으로 풀어보았다.

코드를 작성해보자.

int T = Integer.parseInt(br.readLine());
        
for(int i=0; i<T; i++) {
    String str = br.readLine();
    bw.write(isPalindrome(str, 0)[0]+ " " + isPalindrome(str, 0)[1] + "\n");
}

먼저 테스트케이스 개수 T를 입력받고 테스트케이스 문자열을 입력받는다.
isPalindrom 함수의 인자로 문자열과 호출횟수 0을 넘긴다.

public static int[] isPalindrome(String str, int cnt) {
    return recursion(str, 0, str.length()-1, cnt);
}

isPalindrome 함수의 코드는 다음과 같다. 힌트 코드와 크게 다르지 않지만 호출횟수를 구할 cnt를 추가로 넘겨 recursion 함수를 실행한다.
또한 int형 배열을 통해 반환값을 받아야 하기에 함수의 반환타입을 int형 배열로 변경하였다.

public static int[] recursion(String str, int l, int r, int cnt) {
    cnt++;
    if(l >= r) return new int[] {1, cnt};
    else if(str.charAt(l) != str.charAt(r)) return new int[] {0, cnt};
    else return recursion(str, l+1, r-1, cnt);
}

recursion 함수의 경우 호출횟수 cnt를 1 증가시키고 주어진 문자열이 팰린드롬인지 판별한다. 이 때 int형 배열에 판별여부와 호출횟수를 담아 반환하면 된다.

static 변수 활용

위 코드를 더 가독성 좋게 바꾸기 위해 static 변수를 활용하여 다시 풀어보았다.
static을 사용한다면 메모리에 고정적으로 할당되어 프로그램이 종료될 때 해제되는 변수로 사용할 수 있기 때문에 isPalindrome 함수와 recursion 함수 모두에서 호출횟수 cnt 변수를 생성하지 않아도 된다.

긴말없이 코드부터 먼저 보자.

static int callCnt = 0;

public static int[] recursion(String str, int l, int r, int callCnt) {
    callCnt++;
    if(l >= r) return new int[] {1, callCnt};
    else if(str.charAt(l) != str.charAt(r)) return new int[] {0, callCnt};
    else return recursion(str, l+1, r-1, callCnt);
}

public static int[] isPalindrome(String str) {
    callCnt = 0;
    return recursion(str, 0, str.length()-1, callCnt);
}

static으로 callCnt라는 변수를 선언하고, isPalindrome에서 초기화하고 recursion 함수의 인자로 함께 넘겨준다.
그러면 recursion 함수에서도 callCnt 변수를 알고 있기 때문에 호출횟수를 증가시켜 배열에 담아 반환하게 된다.

작성코드

작성코드

import java.io.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int T = Integer.parseInt(br.readLine());
        
        for(int i=0; i<T; i++) {
            String str = br.readLine();
            bw.write(isPalindrome(str, 0)[0]+ " " + isPalindrome(str, 0)[1] + "\n");
        }
        
        bw.flush();
        bw.close();
        br.close();
    }
    
    public static int[] recursion(String str, int l, int r, int cnt) {
        cnt++;
        if(l >= r) return new int[] {1, cnt};
        else if(str.charAt(l) != str.charAt(r)) return new int[] {0, cnt};
        else return recursion(str, l+1, r-1, cnt);
    }

    public static int[] isPalindrome(String str, int cnt) {
        return recursion(str, 0, str.length()-1, cnt);
    }
}

작성코드 - static 변수 활용

import java.io.*;
import java.util.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int T = Integer.parseInt(br.readLine());
        
        for(int i=0; i<T; i++) {
            String str = br.readLine();
            bw.write(isPalindrome(str)[0]+ " " + isPalindrome(str)[1] + "\n");
        }
        
        bw.flush();
        bw.close();
        br.close();
    }
    
    static int callCnt = 0;

    public static int[] recursion(String str, int l, int r, int callCnt) {
        callCnt++;
        if(l >= r) return new int[] {1, callCnt};
        else if(str.charAt(l) != str.charAt(r)) return new int[] {0, callCnt};
        else return recursion(str, l+1, r-1, callCnt);
    }

    public static int[] isPalindrome(String str) {
        callCnt = 0;
        return recursion(str, 0, str.length()-1, callCnt);
    }
}

회고

• 정적 변수(static 변수)에 대해서 공부하여 불필요한 객체 선언없이 생성된 객체에 접근할 수 있도록 하는 코드를 작성할 수 있었다.